L'autofocus, fonctionnement et limites (Lien)
Sources: Wikipedia, Photozone, Broadcastengineering, Digital Camera Resource Page
On l'a vu dans le post 4 de cet atelier, placer correctement la surface sensible par rapport à l'objectif est capital pour produire une image nette. Autrefois, cette tâche était l'affaire du photographe, mais depuis les années 70, une grande variété de systèmes a été mise au point pour libérer l'utilisateur de ce réglage.
On classe généralement ces systèmes en deux catégories : les autofocus actifs, et les autofocus passifs.
Sources: Wikipedia, Photozone, Broadcastengineering, Digital Camera Resource Page
On l'a vu dans le post 4 de cet atelier, placer correctement la surface sensible par rapport à l'objectif est capital pour produire une image nette. Autrefois, cette tâche était l'affaire du photographe, mais depuis les années 70, une grande variété de systèmes a été mise au point pour libérer l'utilisateur de ce réglage.
On classe généralement ces systèmes en deux catégories : les autofocus actifs, et les autofocus passifs.
Autofocus actifs (Lien)
Comme pour les radars utilisés par les militaires pour localiser leurs ennemis, le qualificatif "actif" signifie qu'il émet un rayonnement pour mesurer la distance avec le sujet. Ce rayonnement peut être infrarouge, ultra-sonore ou même laser.
On ne va pas entrer ici dans les détails techniques du fonctionnement des autofocus actifs, il faut juste savoir qu'ils ont pratiquement disparu avec le numérique, même si certains Bridges comme le F828 de Sony l'ont utilisé.
Leur principal avantage est qu'ils produisent ce qu'ils utilisent pour effectuer leur mesure, ils peuvent donc fonctionner dans le noir complet, et même si le sujet est totalement sombre.
Leur inconvénient est qu'ils sont soit peu discrets (laser), soit la zone sur laquelle est faite la mesure est difficile à déterminer, comme le faisceau infrarouge ou ultrasons est invisible. Enfin, si un objet s'interpose, comme une vitre par exemple, il est fort probable que la mesure se fasse sur cet objet, et non sur le sujet voulu.
Pour ces différentes raisons (et quelques autres), les autofocus actifs ont aujourd'hui presque totalement disparu.
Comme pour les radars utilisés par les militaires pour localiser leurs ennemis, le qualificatif "actif" signifie qu'il émet un rayonnement pour mesurer la distance avec le sujet. Ce rayonnement peut être infrarouge, ultra-sonore ou même laser.
 |  |
|---|---|
| Leica C11 à autofocus Infrarouge | Polaroid 660 à autofocus ultrasons (l'émetteur-récepteur est la pastille dorée) |
 |  |
| Sony DSC-F707 à autofocus Laser | Grille laser crée par l'autofocus du Sony DSC-F707 |
On ne va pas entrer ici dans les détails techniques du fonctionnement des autofocus actifs, il faut juste savoir qu'ils ont pratiquement disparu avec le numérique, même si certains Bridges comme le F828 de Sony l'ont utilisé.
Leur principal avantage est qu'ils produisent ce qu'ils utilisent pour effectuer leur mesure, ils peuvent donc fonctionner dans le noir complet, et même si le sujet est totalement sombre.
Leur inconvénient est qu'ils sont soit peu discrets (laser), soit la zone sur laquelle est faite la mesure est difficile à déterminer, comme le faisceau infrarouge ou ultrasons est invisible. Enfin, si un objet s'interpose, comme une vitre par exemple, il est fort probable que la mesure se fasse sur cet objet, et non sur le sujet voulu.
Pour ces différentes raisons (et quelques autres), les autofocus actifs ont aujourd'hui presque totalement disparu.
Autofocus passifs (Lien)
Dans l'immense majorité des appareils photo d'aujourd'hui, les systèmes de mise au point sont "passif", c'est à dire qu'ils se contentent de la lumière qu'ils reçoivent pour régler correctement la position de la surface sensible afin de former une image nette.
On peut se demander tout d'abord pour quelle raison, et si ce que l'on pense au prime abord est juste : les autofocus passif sont-ils meilleurs que les actifs?
La réponse, vous vous en doutez peut-être, n'est pas si simple.
Si les autofocus passif équipent l'immense majorité des appareils photo d'aujourd'hui, c'est parce qu'ils sont simples, pas cher, et assez efficaces pour ne pas justifier l'ajout d'un système supplémentaire.
Tiens? Et comment ce fait-t-il qu'en se contentant de la lumière reçue, il soit plus simple de faire la mise au point qu'en effectuant une mesure de distance directe?
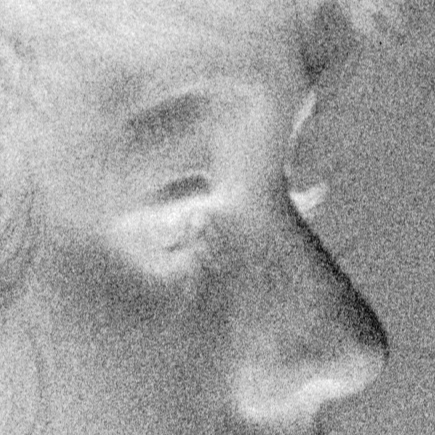
Pour répondre à cette question, examinons deux images, une flou et une nette.
Si on prend les pixels d'une ligne de ces deux images, et que l'on trace une courbe représentant la luminosité de ces pixels tout au long de la ligne, voilà ce qu'on obtient:
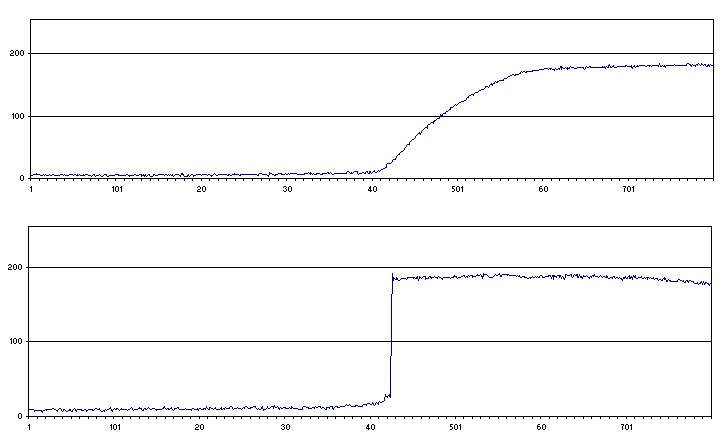 On constate que sur l'image floue, la luminosité varie de façon graduelle, alors que sur l'image nette, cette variation est brutale.
On constate que sur l'image floue, la luminosité varie de façon graduelle, alors que sur l'image nette, cette variation est brutale.
Ainsi, faire la mise au point peut se résumer à essayer de maximiser le contraste de l'image en agissant sur la position de la surface sensible.
À l'époque de l'argentique, il était bien sûr impossible d'examiner l'image qui se formait sur la surface sensible pour en améliorer le contraste, c'est pour cette raison qu'on été mis au point les autofocus dit TTL. L'idée était d'utiliser l'image redirigée vers le viseur par le miroir mobile pour en analyser le contraste.
Sur l'image de gauche ci-dessus, on peut voir le miroir ainsi que le viseur d'un appareil réflex (comme celui de l'image de droite).
Le rayon violet arrivant sur la gauche de l'image de droite est la lumière qui traverse l'objectif. Elle frappe le miroir oblique du réflex pour être ensuite redirigée par le prisme qui la fait ressortir par le viseur dans lequel le photographe a son oeil (rayon jaune). Comme vous le savez sans doute, le propre des "réflexes" est que la visée se fait à travers l'objectif, grâce à un miroir qui se lève au moment où la photo est prise. Et bien c'est le prisme qui redirige la lumière après ce miroir qui va également en envoyer une partie vers le capteur de mise au point TTL (rayon rouge sur l'image de droite). Il pourra ainsi faire son optimisation de contraste à partir d'une partie précise de l'image, déterminée par construction et généralement située au centre de l'image. Comme la lumière utilisé est celle qui sera dirigée vers la surface sensible au moment où sera prise la photo, ce système de mise au point a été appellé "Through The Lens", "à travers l'objectif", par opposition aux autofocus actifs qui sont indépendants de l'optique de l'appareil.
Puis sont apparus les appareils photo numériques, et là tout est devenu plus simple.
Dans les appareils photo numériques, l'image se forme en permanence sur la surface sensible, donc il est possible à n'importe quel moment de l'examiner avec un logiciel. C'est ce que font les autofocus actuels. Ils traitent l'image avec un programme qui va rechercher les ruptures de luminosité comme sur le graphique que l'on vient de voir, et qui vont ensuite essayer de les maximiser en agissant électriquement sur les lentilles de l'objectif (ou la position de la surface sensible).
Cependant, que ce soit par traitement d'image numérique ou capteur TTL, la capacité de l'appareil à faire la mise au point va dépendre du contraste. Les systèmes TTL y seront plus sensible dans la mesure où, du fait de leur construction, ils n'analysent qu'une toute petite partie de l'image, alors que le traitement numérique va porter sur toute la surface. Cependant, dans les deux cas, si l'image a très peu de contraste (souvent le cas en faible lumière où si l'on prend un sujet de couleur parfaitement unie), l'autofocus va "pomper", il cherchera à créer du contraste sans y parvenir. On s'en rend compte car on voit l'appareil parcourir la totalité de la latitude de mise au point sans se fixer. Ceci signifie qu'il faut débrayer l'autofocus et faire le travail soit même...
Dernière remarque sur les systèmes TTL.
On voit sur les réflex numériques actuels que leur technologie est appellée "TTL-CT-SIR", mais qu'est-ce que cela signifie?
Littéralement, TTL-CT-SIR signifie Through The Lens Cross Type Secondary Image Registration. Une telle dénomination suppose une longue suite d'améliorations depuis les premiers TTL, mais ce qui est intéressant de comprendre à leur sujet découle de leur fonctionnement. Celui-ci est décrit ci-dessous:
 Deux optiques disposées après la surface sensible (dans le prisme du viseur) récupèrent et focalisent les rayons issus d'une même zone de l'image, mais ayant traversé l'objectif à deux extrémités. Ces deux optiques crée donc deux images identiques, mais plus ou moins floues et surtout plus ou moins décalées, en fonction de la position des lentilles de l'objectif principal (qui crée l'image pour la surface sensible). Ce décalage est proportionnel et de même sens que la défocalisation de l'image. Ainsi, par la mesure de ce décalage, il est possible de déterminer de combien et dans quel sens déplacer les lentilles de l'objectif pour obtenir la mise au point sur cette partie de l'image. De ce fait, le système d'autofocus n'aura pas à "chercher" la zone de netteté maximum, il pourra déterminer de façon immédiate cette zone, et sera donc d'autant plus rapide. En revanche, même si la rapidité sera optimale, la détermination même du point dépendra de la détection du décalage entre les deux images, et donc de leur contraste.
Deux optiques disposées après la surface sensible (dans le prisme du viseur) récupèrent et focalisent les rayons issus d'une même zone de l'image, mais ayant traversé l'objectif à deux extrémités. Ces deux optiques crée donc deux images identiques, mais plus ou moins floues et surtout plus ou moins décalées, en fonction de la position des lentilles de l'objectif principal (qui crée l'image pour la surface sensible). Ce décalage est proportionnel et de même sens que la défocalisation de l'image. Ainsi, par la mesure de ce décalage, il est possible de déterminer de combien et dans quel sens déplacer les lentilles de l'objectif pour obtenir la mise au point sur cette partie de l'image. De ce fait, le système d'autofocus n'aura pas à "chercher" la zone de netteté maximum, il pourra déterminer de façon immédiate cette zone, et sera donc d'autant plus rapide. En revanche, même si la rapidité sera optimale, la détermination même du point dépendra de la détection du décalage entre les deux images, et donc de leur contraste.
Aussi, même si les systèmes TTL-CT-SIR sont les plus rapides, ils sont néanmoins dépendant du niveau de contraste de la scène sur laquelle ils doivent faire le point.
Enfin, comme les systèmes de mise au point TTL utilisent deux images issues de deux extrémités de l'optique, plus celle-ci sera grande, plus leur fonctionnement sera efficace. Cependant, comme tout système de mesure, il y a une limite au delà de laquelle la mise au point n'est plus possible, à cause de la taille trop réduite de la lentille principale. Cette limite est proportionnelle à la focale (car la focale ainsi que le système TTL sont dimensionnés en rapport avec la taille de la surface sensible). De fait, on peut exprimer la limite de fonctionnement de l'autofocus TTL comme un nombre d'ouverture. Lorsqu'on regarde dans les documentations des boîtiers réflex, on constate généralement que le fonctionnement des autofocus TTL est garanti jusqu'à f/5.6, même si certains fonctionnent encore jusqu'à f/8. Bien évidemment, aucun objectif n'est incompatible avec cette limite, car il serait alors pratiquement invendable, mais il faut y prêter attention si l'on utilise un doubleur (ou "teleconverter"). Comme ces équipements font diverger les rayons sortant de l'objectif, ils reproduisent l'effet d'une diminution du nombre d'ouverture. Par conséquent, leur utilisation peut mettre hors d'usage un autofocus. Si vous monter par exemple un doubleur de focale sur un zoom qui ouvre à f/5.6 à sa plus longue focale, cela donnera un f/11 avec le doubleur, et dans ces conditions aucun autofocus TTL ne pourra faire la mise au point, et vous devrez alors la faire manuellement.
Dans l'immense majorité des appareils photo d'aujourd'hui, les systèmes de mise au point sont "passif", c'est à dire qu'ils se contentent de la lumière qu'ils reçoivent pour régler correctement la position de la surface sensible afin de former une image nette.
On peut se demander tout d'abord pour quelle raison, et si ce que l'on pense au prime abord est juste : les autofocus passif sont-ils meilleurs que les actifs?
La réponse, vous vous en doutez peut-être, n'est pas si simple.
Si les autofocus passif équipent l'immense majorité des appareils photo d'aujourd'hui, c'est parce qu'ils sont simples, pas cher, et assez efficaces pour ne pas justifier l'ajout d'un système supplémentaire.
Tiens? Et comment ce fait-t-il qu'en se contentant de la lumière reçue, il soit plus simple de faire la mise au point qu'en effectuant une mesure de distance directe?
Pour répondre à cette question, examinons deux images, une flou et une nette.
 |  |
|---|
Si on prend les pixels d'une ligne de ces deux images, et que l'on trace une courbe représentant la luminosité de ces pixels tout au long de la ligne, voilà ce qu'on obtient:
 On constate que sur l'image floue, la luminosité varie de façon graduelle, alors que sur l'image nette, cette variation est brutale.
On constate que sur l'image floue, la luminosité varie de façon graduelle, alors que sur l'image nette, cette variation est brutale.Ainsi, faire la mise au point peut se résumer à essayer de maximiser le contraste de l'image en agissant sur la position de la surface sensible.
À l'époque de l'argentique, il était bien sûr impossible d'examiner l'image qui se formait sur la surface sensible pour en améliorer le contraste, c'est pour cette raison qu'on été mis au point les autofocus dit TTL. L'idée était d'utiliser l'image redirigée vers le viseur par le miroir mobile pour en analyser le contraste.
 |  |
|---|---|
| Système d'autofocus TTL d'un Réflex Nikon | Structure d'un réflex Canon EOS 450D |
Sur l'image de gauche ci-dessus, on peut voir le miroir ainsi que le viseur d'un appareil réflex (comme celui de l'image de droite).
Le rayon violet arrivant sur la gauche de l'image de droite est la lumière qui traverse l'objectif. Elle frappe le miroir oblique du réflex pour être ensuite redirigée par le prisme qui la fait ressortir par le viseur dans lequel le photographe a son oeil (rayon jaune). Comme vous le savez sans doute, le propre des "réflexes" est que la visée se fait à travers l'objectif, grâce à un miroir qui se lève au moment où la photo est prise. Et bien c'est le prisme qui redirige la lumière après ce miroir qui va également en envoyer une partie vers le capteur de mise au point TTL (rayon rouge sur l'image de droite). Il pourra ainsi faire son optimisation de contraste à partir d'une partie précise de l'image, déterminée par construction et généralement située au centre de l'image. Comme la lumière utilisé est celle qui sera dirigée vers la surface sensible au moment où sera prise la photo, ce système de mise au point a été appellé "Through The Lens", "à travers l'objectif", par opposition aux autofocus actifs qui sont indépendants de l'optique de l'appareil.
Puis sont apparus les appareils photo numériques, et là tout est devenu plus simple.
Dans les appareils photo numériques, l'image se forme en permanence sur la surface sensible, donc il est possible à n'importe quel moment de l'examiner avec un logiciel. C'est ce que font les autofocus actuels. Ils traitent l'image avec un programme qui va rechercher les ruptures de luminosité comme sur le graphique que l'on vient de voir, et qui vont ensuite essayer de les maximiser en agissant électriquement sur les lentilles de l'objectif (ou la position de la surface sensible).
Cependant, que ce soit par traitement d'image numérique ou capteur TTL, la capacité de l'appareil à faire la mise au point va dépendre du contraste. Les systèmes TTL y seront plus sensible dans la mesure où, du fait de leur construction, ils n'analysent qu'une toute petite partie de l'image, alors que le traitement numérique va porter sur toute la surface. Cependant, dans les deux cas, si l'image a très peu de contraste (souvent le cas en faible lumière où si l'on prend un sujet de couleur parfaitement unie), l'autofocus va "pomper", il cherchera à créer du contraste sans y parvenir. On s'en rend compte car on voit l'appareil parcourir la totalité de la latitude de mise au point sans se fixer. Ceci signifie qu'il faut débrayer l'autofocus et faire le travail soit même...
Dernière remarque sur les systèmes TTL.
On voit sur les réflex numériques actuels que leur technologie est appellée "TTL-CT-SIR", mais qu'est-ce que cela signifie?
Littéralement, TTL-CT-SIR signifie Through The Lens Cross Type Secondary Image Registration. Une telle dénomination suppose une longue suite d'améliorations depuis les premiers TTL, mais ce qui est intéressant de comprendre à leur sujet découle de leur fonctionnement. Celui-ci est décrit ci-dessous:
 Deux optiques disposées après la surface sensible (dans le prisme du viseur) récupèrent et focalisent les rayons issus d'une même zone de l'image, mais ayant traversé l'objectif à deux extrémités. Ces deux optiques crée donc deux images identiques, mais plus ou moins floues et surtout plus ou moins décalées, en fonction de la position des lentilles de l'objectif principal (qui crée l'image pour la surface sensible). Ce décalage est proportionnel et de même sens que la défocalisation de l'image. Ainsi, par la mesure de ce décalage, il est possible de déterminer de combien et dans quel sens déplacer les lentilles de l'objectif pour obtenir la mise au point sur cette partie de l'image. De ce fait, le système d'autofocus n'aura pas à "chercher" la zone de netteté maximum, il pourra déterminer de façon immédiate cette zone, et sera donc d'autant plus rapide. En revanche, même si la rapidité sera optimale, la détermination même du point dépendra de la détection du décalage entre les deux images, et donc de leur contraste.
Deux optiques disposées après la surface sensible (dans le prisme du viseur) récupèrent et focalisent les rayons issus d'une même zone de l'image, mais ayant traversé l'objectif à deux extrémités. Ces deux optiques crée donc deux images identiques, mais plus ou moins floues et surtout plus ou moins décalées, en fonction de la position des lentilles de l'objectif principal (qui crée l'image pour la surface sensible). Ce décalage est proportionnel et de même sens que la défocalisation de l'image. Ainsi, par la mesure de ce décalage, il est possible de déterminer de combien et dans quel sens déplacer les lentilles de l'objectif pour obtenir la mise au point sur cette partie de l'image. De ce fait, le système d'autofocus n'aura pas à "chercher" la zone de netteté maximum, il pourra déterminer de façon immédiate cette zone, et sera donc d'autant plus rapide. En revanche, même si la rapidité sera optimale, la détermination même du point dépendra de la détection du décalage entre les deux images, et donc de leur contraste.Aussi, même si les systèmes TTL-CT-SIR sont les plus rapides, ils sont néanmoins dépendant du niveau de contraste de la scène sur laquelle ils doivent faire le point.
Enfin, comme les systèmes de mise au point TTL utilisent deux images issues de deux extrémités de l'optique, plus celle-ci sera grande, plus leur fonctionnement sera efficace. Cependant, comme tout système de mesure, il y a une limite au delà de laquelle la mise au point n'est plus possible, à cause de la taille trop réduite de la lentille principale. Cette limite est proportionnelle à la focale (car la focale ainsi que le système TTL sont dimensionnés en rapport avec la taille de la surface sensible). De fait, on peut exprimer la limite de fonctionnement de l'autofocus TTL comme un nombre d'ouverture. Lorsqu'on regarde dans les documentations des boîtiers réflex, on constate généralement que le fonctionnement des autofocus TTL est garanti jusqu'à f/5.6, même si certains fonctionnent encore jusqu'à f/8. Bien évidemment, aucun objectif n'est incompatible avec cette limite, car il serait alors pratiquement invendable, mais il faut y prêter attention si l'on utilise un doubleur (ou "teleconverter"). Comme ces équipements font diverger les rayons sortant de l'objectif, ils reproduisent l'effet d'une diminution du nombre d'ouverture. Par conséquent, leur utilisation peut mettre hors d'usage un autofocus. Si vous monter par exemple un doubleur de focale sur un zoom qui ouvre à f/5.6 à sa plus longue focale, cela donnera un f/11 avec le doubleur, et dans ces conditions aucun autofocus TTL ne pourra faire la mise au point, et vous devrez alors la faire manuellement.
La perception des couleurs (Lien)
Sources: Colorimétrie, étude de la couleur, Wikipédia, profil-couleur.com
La question de la nature de la couleur est bien plus ancienne que l'invention de l'autochrome, le premier procédé industriel de photographie couleur, par Louis Lumière au début du XXème siècle.
Presque philosophiquement, les Hommes, depuis Aristote, se sont demandés si les couleurs étaient des réalités objectives, ou des créations de notre esprit. Celui-ci faisait même la distinction entre les concepts de "couleur-lumière" et "couleur-matière", supposant ainsi que les lumières colorées (comme celles d'un coucher de soleil), et les objets colorés ne mettaient pas en oeuvre les mêmes phénomènes.
Il faudra attendre les théories de Newton au XVIIème puis celles de Young au XVIIIème pour arriver à la conception que l'on a encore aujourd'hui de la nature de la couleur.
La couleur est une information électrique provenant des cônes qui tapissent la fovéa de notre oeil. Cette information est créée à partir de l'interaction entre les ondes électro-magnétiques qui forment la lumière et les trois types de cônes que nous possédons. La fovéa, comme on en a déjà parlé au début de la partie 2, est la partie du fond de l'oeil qui contient les récepteurs nous fournissant notre acuité visuelle et la distinction des couleurs.
La lumière, comme le son, est une onde.
Cependant, une onde, comme une vague à la surface de l'eau, ne peut être entièrement appréhendée que si on perçoit son aspect de profil sur toute sa longueur. Pour les sons, les cils situés à l'intérieur de notre oreille vibrent avec l'onde sonore, nous transmettant ainsi toute sa forme au fur et à mesure qu'elle nous parvient. Pour la lumière, les cônes ne sont pas capables d'une telle résolution, ils se comportent comme un flotteur à la surface de l'eau dont on ne verrait que l'amplitude de l'oscillation sous l'effet de l'onde qui l'agite. Un tel mécanisme de perception nous fait perdre une grande partie de l'information que contient l'onde, mais la nature l'a conservé car il était suffisant à la survie de notre espèce.
Ainsi, les couleurs que l'on perçoit sont issues de l'amplitude de l'oscillation des trois types de cônes que contiennent nos yeux, les rouges, les verts, et les bleus. Ces cônes sont nommés ainsi car leur amplitude d'oscillation est maximum pour les ondes électro-magnétiques correspondantes aux lumières de couleurs pures rouge, vert et bleu.
Très bien. Mais alors, que se passe-t-il lorsque je regarde un objet qui m'apparaît jaune?
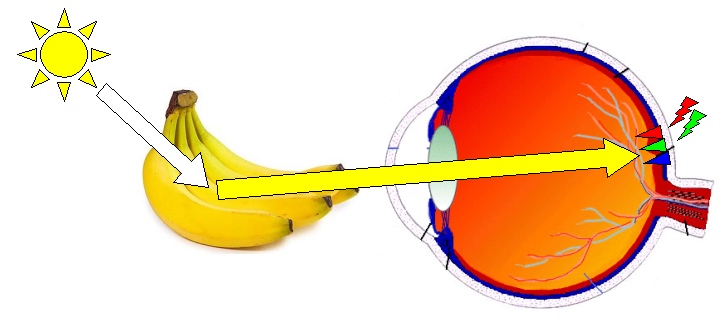
L'objet en question est éclairé par une source lumineuse, comme le soleil par exemple. Il émet une onde électro-magnétique irrégulière et complexe, contenant entre autres de la lumière blanche. Au contact de l'objet jaune (une banane par exemple), une partie de ce rayonnement va être absorbé, et une partie va être renvoyé, un peu comme une onde à la surface d'une piscine qui rebondit sur le rebord pour continuer à se propager vers le milieu du bassin. L'onde réfléchit va être différente de celle reçue, car la façon dont l'objet va la modifier variera en fonction de celui-ci mais aussi de la forme de l'onde qui l'a atteint. Ainsi, si l'objet est jaune, l'onde réfléchit sera beaucoup plus simple que celle reçue et sa forme aura pour effet de ne faire osciller que les cônes rouge et vert de notre oeil.
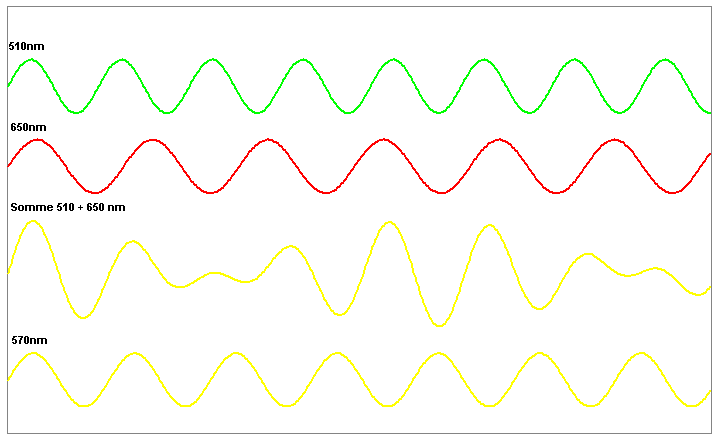 Les courbes rouge et vert représentent les ondes électo-magnétiques qui créeront le maximum d'amplitude d'oscillation des cônes rouges et verts de la fovéa. L'onde jaune réfléchie par la banane aura pour effet de ne faire osciller que les cônes rouges et verts, produisant ainsi l'impression de jaune. Cependant, plusieurs ondes de formes différentes pourront avoir le même effet sur les trois types de cônes de l'oeil, c'est ce que montre la figure ci-dessus. On appelle ce phénomène le métamérisme, il s'explique par la mécanique vibratoire.
Les courbes rouge et vert représentent les ondes électo-magnétiques qui créeront le maximum d'amplitude d'oscillation des cônes rouges et verts de la fovéa. L'onde jaune réfléchie par la banane aura pour effet de ne faire osciller que les cônes rouges et verts, produisant ainsi l'impression de jaune. Cependant, plusieurs ondes de formes différentes pourront avoir le même effet sur les trois types de cônes de l'oeil, c'est ce que montre la figure ci-dessus. On appelle ce phénomène le métamérisme, il s'explique par la mécanique vibratoire.
Si vous voulez faire rebondir un ballon de basket immobile sur le sol en tapant dessus, vous devrez le frapper à la bonne fréquence, sinon le ballon ne s'élèvera pas. C'est la même chose pour les cônes de l'oeil. Ils n'enregistrent que l'amplitude du rebond, mais pas le mouvement de la main qui frappe le ballon. Pour cette raison, que l'onde soit une sinusoïde de 570nm de longueur d'onde ou la somme de deux sinusoïdes de 650 et 510nm, l'impression sera la même pour l'oeil car les amplitudes des signaux électriques créés par les cônes seront les mêmes.
Sources: Colorimétrie, étude de la couleur, Wikipédia, profil-couleur.com
La question de la nature de la couleur est bien plus ancienne que l'invention de l'autochrome, le premier procédé industriel de photographie couleur, par Louis Lumière au début du XXème siècle.
Presque philosophiquement, les Hommes, depuis Aristote, se sont demandés si les couleurs étaient des réalités objectives, ou des créations de notre esprit. Celui-ci faisait même la distinction entre les concepts de "couleur-lumière" et "couleur-matière", supposant ainsi que les lumières colorées (comme celles d'un coucher de soleil), et les objets colorés ne mettaient pas en oeuvre les mêmes phénomènes.
Il faudra attendre les théories de Newton au XVIIème puis celles de Young au XVIIIème pour arriver à la conception que l'on a encore aujourd'hui de la nature de la couleur.
La couleur est une information électrique provenant des cônes qui tapissent la fovéa de notre oeil. Cette information est créée à partir de l'interaction entre les ondes électro-magnétiques qui forment la lumière et les trois types de cônes que nous possédons. La fovéa, comme on en a déjà parlé au début de la partie 2, est la partie du fond de l'oeil qui contient les récepteurs nous fournissant notre acuité visuelle et la distinction des couleurs.
La lumière, comme le son, est une onde.
Cependant, une onde, comme une vague à la surface de l'eau, ne peut être entièrement appréhendée que si on perçoit son aspect de profil sur toute sa longueur. Pour les sons, les cils situés à l'intérieur de notre oreille vibrent avec l'onde sonore, nous transmettant ainsi toute sa forme au fur et à mesure qu'elle nous parvient. Pour la lumière, les cônes ne sont pas capables d'une telle résolution, ils se comportent comme un flotteur à la surface de l'eau dont on ne verrait que l'amplitude de l'oscillation sous l'effet de l'onde qui l'agite. Un tel mécanisme de perception nous fait perdre une grande partie de l'information que contient l'onde, mais la nature l'a conservé car il était suffisant à la survie de notre espèce.
Ainsi, les couleurs que l'on perçoit sont issues de l'amplitude de l'oscillation des trois types de cônes que contiennent nos yeux, les rouges, les verts, et les bleus. Ces cônes sont nommés ainsi car leur amplitude d'oscillation est maximum pour les ondes électro-magnétiques correspondantes aux lumières de couleurs pures rouge, vert et bleu.
Très bien. Mais alors, que se passe-t-il lorsque je regarde un objet qui m'apparaît jaune?

L'objet en question est éclairé par une source lumineuse, comme le soleil par exemple. Il émet une onde électro-magnétique irrégulière et complexe, contenant entre autres de la lumière blanche. Au contact de l'objet jaune (une banane par exemple), une partie de ce rayonnement va être absorbé, et une partie va être renvoyé, un peu comme une onde à la surface d'une piscine qui rebondit sur le rebord pour continuer à se propager vers le milieu du bassin. L'onde réfléchit va être différente de celle reçue, car la façon dont l'objet va la modifier variera en fonction de celui-ci mais aussi de la forme de l'onde qui l'a atteint. Ainsi, si l'objet est jaune, l'onde réfléchit sera beaucoup plus simple que celle reçue et sa forme aura pour effet de ne faire osciller que les cônes rouge et vert de notre oeil.
 Les courbes rouge et vert représentent les ondes électo-magnétiques qui créeront le maximum d'amplitude d'oscillation des cônes rouges et verts de la fovéa. L'onde jaune réfléchie par la banane aura pour effet de ne faire osciller que les cônes rouges et verts, produisant ainsi l'impression de jaune. Cependant, plusieurs ondes de formes différentes pourront avoir le même effet sur les trois types de cônes de l'oeil, c'est ce que montre la figure ci-dessus. On appelle ce phénomène le métamérisme, il s'explique par la mécanique vibratoire.
Les courbes rouge et vert représentent les ondes électo-magnétiques qui créeront le maximum d'amplitude d'oscillation des cônes rouges et verts de la fovéa. L'onde jaune réfléchie par la banane aura pour effet de ne faire osciller que les cônes rouges et verts, produisant ainsi l'impression de jaune. Cependant, plusieurs ondes de formes différentes pourront avoir le même effet sur les trois types de cônes de l'oeil, c'est ce que montre la figure ci-dessus. On appelle ce phénomène le métamérisme, il s'explique par la mécanique vibratoire.Si vous voulez faire rebondir un ballon de basket immobile sur le sol en tapant dessus, vous devrez le frapper à la bonne fréquence, sinon le ballon ne s'élèvera pas. C'est la même chose pour les cônes de l'oeil. Ils n'enregistrent que l'amplitude du rebond, mais pas le mouvement de la main qui frappe le ballon. Pour cette raison, que l'onde soit une sinusoïde de 570nm de longueur d'onde ou la somme de deux sinusoïdes de 650 et 510nm, l'impression sera la même pour l'oeil car les amplitudes des signaux électriques créés par les cônes seront les mêmes.
Notions de colorimétrie (Lien)
Sources: L'infographie, un métier, une passion, Collège National des Enseignants de Biophysique et de Médecine Nucléaire, Wikipedia
Comme on vient de le voir, il n'est pas aisé de définir le rapport entre une onde électro-magnétique clairement définissable, et l'impression que notre oeil aura lors de sa perception.
Comme il était nécessaire pour communiquer de standardiser la représentation des couleurs en dehors de toute perception subjective, plusieurs modèles, aussi appelés espaces colorimétriques, ont été mis au point.
Voici le plus connu et le plus utilisé de ces modèles, la référence en quelque sorte, le CIE xyY de 1931 (hé oui, on a pas fait mieux depuis).
Pour bâtir ce modèle, la Commission Internationale de l'Eclairage (d'où le nom CIE) a défini trois modèles pour les trois cônes de l'oeil. Ce sont des formules mathématiques permettant de calculer l'amplitude d'oscillation de ceux-ci lorsqu'on connaît la forme de l'onde qui les atteint. À partir de ces formules, les scientifiques de la commission ont déterminé dans quelles plages d'amplitude d'oscillation de chacun des trois cônes l'oeil percevait une couleur. Comme il n'est pas possible de représenter les effets de trois paramètres dans un plan (un volume en trois dimensions est indispensable pour cela), la CIE a créé une représentation de ces résultats en ne montrant que les rapport entre ces trois paramètres, et non leur valeur absolue, un peu comme on peut représenter la valeur de trois masses en prenant leur somme comme référence égale à 1.
Voici ce que donne cette représentation:
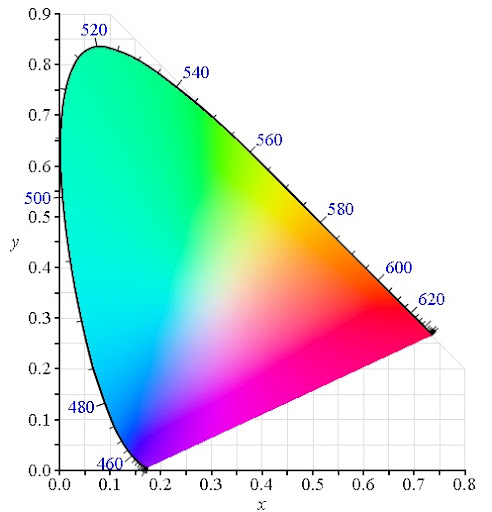 L'axe y représente l'amplitude de l'oscillation du cône vert par rapport à la somme des trois amplitudes. Autrement dit, 0,3 sur l'axe y représente toutes les couleurs pour lesquelles le cône vert fournira 30% de l'amplitude totale du signal électrique issu des trois cônes.
L'axe y représente l'amplitude de l'oscillation du cône vert par rapport à la somme des trois amplitudes. Autrement dit, 0,3 sur l'axe y représente toutes les couleurs pour lesquelles le cône vert fournira 30% de l'amplitude totale du signal électrique issu des trois cônes.
L'axe x représente l'amplitude de l'oscillation du cône rouge par rapport à la somme des trois amplitudes.
Le cône bleu, lui, fournira l'amplitude restante. Par exemple, le point de ce diagramme qui a pour coordonnées y=0,3 et x=0,6 aura 30% du signal fourni par le cône vert, 60% par le rouge et 100-30-60=10% par le bleu. Comme on peut le voir sur ce diagramme, ce point est dans la zone de couleur rouge, on dira donc que cette onde aura une chrominance rouge.
D'accord, on a donc une figure qui nous donne la couleur en fonction du rapport des amplitudes d'oscillation des trois cônes, mais pourquoi toutes les valeurs ne sont pas possible, que se passe-t-il si il n'y a que le cône bleu qui produit un signal par exemple? On devrait être à x=y=0, et dans cette zone du graphique on est en dehors de la figure colorée, comment cela se fait-t-il?
La réponse à cette question se trouve dans ce graphique:
 Ces courbes représentent l'amplitude d'oscillation des cônes en fonction de la longueur d'onde du rayonnement qui les atteignent. Ce sont les fameux modèles des trois cônes de l'oeil que la CIE a bâti. Que voit-on grâce à eux? On voit qu'il est impossible de faire osciller un seul des trois cônes. Pour toutes les longueurs d'ondes de la lumière visible (celles qui font osciller au moins un des trois cônes), au moins deux cônes oscillent, à des amplitudes différentes certes, mais ils oscillent tout de même.
Ces courbes représentent l'amplitude d'oscillation des cônes en fonction de la longueur d'onde du rayonnement qui les atteignent. Ce sont les fameux modèles des trois cônes de l'oeil que la CIE a bâti. Que voit-on grâce à eux? On voit qu'il est impossible de faire osciller un seul des trois cônes. Pour toutes les longueurs d'ondes de la lumière visible (celles qui font osciller au moins un des trois cônes), au moins deux cônes oscillent, à des amplitudes différentes certes, mais ils oscillent tout de même.
Pour cette raison, le digramme coloré du CIE qui figure plus haut possède des zones qui ne correspondent à rien. Tout simplement parce qu'il est impossible de générer une onde, si complexe soit-elle, qui fera osciller les trois cônes selon le rapport correspondant à ce point du diagramme (x=y=0 ne correspond à rien car aucune onde ne pourra faire osciller le cône bleu tout seul).
Autre particularité de ce diagramme: Quelle est cette bordure qui fait le tour de la zone colorée par le haut et qui est graduée avec des nombres allant de 460 à 620?
C'est la limite du rapport d'oscillation des trois cônes correspondant aux fréquences purs (les ondes à forme sinusoïdale). La graduation représente quand à elle la longueur de ces ondes en nanomètre (le milliardième de mètre).
Autre curiosité, la limite basse de cette zone colorée n'est pas graduée. Ceci vient du fait que ces rapports d'amplitudes d'oscillation des cônes ne peuvent être obtenu, contrairement à la limite haute graduée, avec des ondes de forme sinusoïdale. Un peu comme l'onde de forme irrégulière donnant une sensation de jaune qu'on a vu à propos de la couleur de la banane. La ligne des pourpres, comme on l'appelle, ne contient que des couleurs qu'on ne peut créer avec de simples sinusoïdes, mais uniquement avec des formes d'onde plus complexes.
Maintenant que l'on a compris à quoi correspond l'espace colorimétrique CIE xyY de 1931, on va pouvoir voir à quoi il sert.
Cet espace contient toutes les chrominances que l'oeil humain est capable de percevoir (on dit chrominance car on ne s'intéresse pas à l'intensité de la lumière, uniquement à sa couleur). Il peut donc servir à mettre en évidence les limitations des systèmes représentant des couleurs.
Voici quelques-uns de ces systèmes:
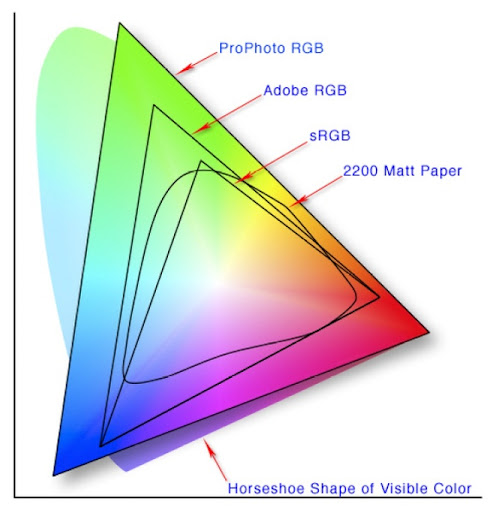 On retrouve ici le CIE xyY sous le nom de "Horseshoes Shape of Visible Color", en français: "sabot de cheval des couleurs visibles", à cause de sa forme. Les quatre autres zone, triangulaires pour trois d'entre elles, représentent d'autres espaces colorimétriques.
On retrouve ici le CIE xyY sous le nom de "Horseshoes Shape of Visible Color", en français: "sabot de cheval des couleurs visibles", à cause de sa forme. Les quatre autres zone, triangulaires pour trois d'entre elles, représentent d'autres espaces colorimétriques.
ProPhoto RGB, Adobe RGB et sRGB sont des systèmes de codages de la couleur utilisés en informatique. Nous en reparlerons plus en détails dans le post suivant au sujet du stockage numérique des images. Vous les avez peut-être aperçu comme paramètres de réglage si vous utilisez Photoshop. Ce diagramme permet de mettre en évidence leur limitations respectives. Par exemple, il est des couleurs qui seront codables en ProPhoto RBG, mais qu'il sera impossible de représenter en sRGB, un peu comme lorsque vous devez vous contenter d'une couleur approchante lorsque vous ne trouvez pas la teinte déjà passée dans un appartement dont vous voulez ne refaire qu'un seul mur.
La zone "2200 Matt Paper" est très intéressante car, contrairement aux trois autres qui correspondent à des systèmes de codage des couleurs, elle correspond à un phénomène physique tangible.
Savez-vous comment on fait pour donner une couleur à un objet? On y passe de la peinture bien sûr, mais on y dépose surtout des pigments qui vont absorber certaines longueurs d'ondes et en renvoyer d'autres. Comme la banane dont on a déjà parlé, les pigments de peinture modifient l'onde reçue pour en renvoyer une différente. Comme tous les rayonnements électro-magnétiques, les ondes sont périodiques et on peut les décomposer mathématiquement en une somme de sinusoïdes de différentes périodes (comme l'onde jaune bizarre qu'on a vu plus haut comme étant la somme des sinusoïdes verte et rouge). L'onde renvoyée par une surface sur laquelle on a appliqué des pigments peut donc être vue comme la somme d'un ensemble de sinusoïdes. Le phénomène physique de l'absorption fait que les pigments ne pourront que diminuer le nombre de sinusoïdes qui composent le rayonnement qu'ils vont réfléchir. De ce fait, on parle de synthèse soustractive de la couleur, car les pigments enlèvent des fréquences et ne peuvent en ajouter dans le rayonnement qu'ils renvoient.
Ainsi, en choisissant les pigments que l'on va déposer sur un objet ou une feuille, on peut produire différentes couleurs, mais pas autant que ce que l'oeil peut en percevoir. C'est ce que montre la zone appelée "2200 Matt Paper". Avec une impression sur papier glacé, il ne sera pas possible de reproduire toutes les couleurs que l'appareil photo aura pu saisir avec son capteur, car les couleurs obtenues sur le papier le sont par synthèse soustractive.
Autre remarque et pas des moindre à propos de ce diagramme CIE xyY coloré : l'écran de votre ordinateur, tout comme l'impression papier, possède ses propres limites dans l'affichage des couleurs. Elles sont d'ailleurs assez proche du système sRVB. Aussi, les couleurs que vous voyez dans ce diagramme en dehors de la zone sRVB ne sont que purement illustratives. Votre moniteur d'ordinateur, et les images JPG représentant ce diagramme, utilisent le système sRGB, il leur est par conséquent impossible de représenter les couleurs hors de cette zone. Pour cette raison, celles qui y sont affichées ne correspondent pas aux couleurs qui se trouvent réellement à cet endroit dans l'espace CIE xyY.
Si vous voulez constater vous même à quoi correspondent les limitations des appareils photo et des écrans LCD en matière de rendu des couleurs, il existe une expérience simple. Photographiez un coucher de soleil avec un appareil photo numérique, puis affichez immédiatement cette photo sur l'écran de de l'appareil et comparez les couleurs à celles du vrai coucher de soleil que vous avez encore devant vos yeux. Le résultat est saisissant. Si la plupart des couleurs que nous voyons tous les jours sont le fruit de la synthèse soustractive de la lumière (car tous les objets produisent leur couleur par synthèse soustractive), ce n'est pas le cas d'un coucher de soleil, qui nous envoi la lumière de notre étoile modifiée et filtrée par l'atmosphère terrestre. De ce fait, la plage des couleurs possible est incroyablement plus étendue, et les appareils photo, mais surtout les écrans LCD, sont alors incapables de restituer une telle gamme de couleurs.
Enfin, si vous voulez savoir si votre navigateur web gère correctement ces différents espaces colorimétriques, il y a cette page qui permet de faire un test très efficace pour le vérifier. L'image de droite est un repère, lorsque vous passez la souris dessus, quel que soit votre navigateur, les couleurs changent car l'espace colorimétrique utilisé change. La photo de gauche est le test : si ses couleurs changent lors vous passez la souris dessus (comme pour l'image de droite), c'est que votre navigateur ne gère pas correctement les espaces colorimétriques. Si c'est le cas, vous ne vous en êtes sans doute jamais rendu compte, mais cela veux dire que vous courez le risque d'avoir de fausses couleurs pour certaines photos des pages web, toutes celles qui ne sont pas codées dans l'espace sRGB en fait, car c'est celui utilisé par défaut par les navigateurs.
Sources: L'infographie, un métier, une passion, Collège National des Enseignants de Biophysique et de Médecine Nucléaire, Wikipedia
Comme on vient de le voir, il n'est pas aisé de définir le rapport entre une onde électro-magnétique clairement définissable, et l'impression que notre oeil aura lors de sa perception.
Comme il était nécessaire pour communiquer de standardiser la représentation des couleurs en dehors de toute perception subjective, plusieurs modèles, aussi appelés espaces colorimétriques, ont été mis au point.
Voici le plus connu et le plus utilisé de ces modèles, la référence en quelque sorte, le CIE xyY de 1931 (hé oui, on a pas fait mieux depuis).
Pour bâtir ce modèle, la Commission Internationale de l'Eclairage (d'où le nom CIE) a défini trois modèles pour les trois cônes de l'oeil. Ce sont des formules mathématiques permettant de calculer l'amplitude d'oscillation de ceux-ci lorsqu'on connaît la forme de l'onde qui les atteint. À partir de ces formules, les scientifiques de la commission ont déterminé dans quelles plages d'amplitude d'oscillation de chacun des trois cônes l'oeil percevait une couleur. Comme il n'est pas possible de représenter les effets de trois paramètres dans un plan (un volume en trois dimensions est indispensable pour cela), la CIE a créé une représentation de ces résultats en ne montrant que les rapport entre ces trois paramètres, et non leur valeur absolue, un peu comme on peut représenter la valeur de trois masses en prenant leur somme comme référence égale à 1.
Voici ce que donne cette représentation:
 L'axe y représente l'amplitude de l'oscillation du cône vert par rapport à la somme des trois amplitudes. Autrement dit, 0,3 sur l'axe y représente toutes les couleurs pour lesquelles le cône vert fournira 30% de l'amplitude totale du signal électrique issu des trois cônes.
L'axe y représente l'amplitude de l'oscillation du cône vert par rapport à la somme des trois amplitudes. Autrement dit, 0,3 sur l'axe y représente toutes les couleurs pour lesquelles le cône vert fournira 30% de l'amplitude totale du signal électrique issu des trois cônes.L'axe x représente l'amplitude de l'oscillation du cône rouge par rapport à la somme des trois amplitudes.
Le cône bleu, lui, fournira l'amplitude restante. Par exemple, le point de ce diagramme qui a pour coordonnées y=0,3 et x=0,6 aura 30% du signal fourni par le cône vert, 60% par le rouge et 100-30-60=10% par le bleu. Comme on peut le voir sur ce diagramme, ce point est dans la zone de couleur rouge, on dira donc que cette onde aura une chrominance rouge.
D'accord, on a donc une figure qui nous donne la couleur en fonction du rapport des amplitudes d'oscillation des trois cônes, mais pourquoi toutes les valeurs ne sont pas possible, que se passe-t-il si il n'y a que le cône bleu qui produit un signal par exemple? On devrait être à x=y=0, et dans cette zone du graphique on est en dehors de la figure colorée, comment cela se fait-t-il?
La réponse à cette question se trouve dans ce graphique:
 Ces courbes représentent l'amplitude d'oscillation des cônes en fonction de la longueur d'onde du rayonnement qui les atteignent. Ce sont les fameux modèles des trois cônes de l'oeil que la CIE a bâti. Que voit-on grâce à eux? On voit qu'il est impossible de faire osciller un seul des trois cônes. Pour toutes les longueurs d'ondes de la lumière visible (celles qui font osciller au moins un des trois cônes), au moins deux cônes oscillent, à des amplitudes différentes certes, mais ils oscillent tout de même.
Ces courbes représentent l'amplitude d'oscillation des cônes en fonction de la longueur d'onde du rayonnement qui les atteignent. Ce sont les fameux modèles des trois cônes de l'oeil que la CIE a bâti. Que voit-on grâce à eux? On voit qu'il est impossible de faire osciller un seul des trois cônes. Pour toutes les longueurs d'ondes de la lumière visible (celles qui font osciller au moins un des trois cônes), au moins deux cônes oscillent, à des amplitudes différentes certes, mais ils oscillent tout de même.Pour cette raison, le digramme coloré du CIE qui figure plus haut possède des zones qui ne correspondent à rien. Tout simplement parce qu'il est impossible de générer une onde, si complexe soit-elle, qui fera osciller les trois cônes selon le rapport correspondant à ce point du diagramme (x=y=0 ne correspond à rien car aucune onde ne pourra faire osciller le cône bleu tout seul).
Autre particularité de ce diagramme: Quelle est cette bordure qui fait le tour de la zone colorée par le haut et qui est graduée avec des nombres allant de 460 à 620?
C'est la limite du rapport d'oscillation des trois cônes correspondant aux fréquences purs (les ondes à forme sinusoïdale). La graduation représente quand à elle la longueur de ces ondes en nanomètre (le milliardième de mètre).
Autre curiosité, la limite basse de cette zone colorée n'est pas graduée. Ceci vient du fait que ces rapports d'amplitudes d'oscillation des cônes ne peuvent être obtenu, contrairement à la limite haute graduée, avec des ondes de forme sinusoïdale. Un peu comme l'onde de forme irrégulière donnant une sensation de jaune qu'on a vu à propos de la couleur de la banane. La ligne des pourpres, comme on l'appelle, ne contient que des couleurs qu'on ne peut créer avec de simples sinusoïdes, mais uniquement avec des formes d'onde plus complexes.
Maintenant que l'on a compris à quoi correspond l'espace colorimétrique CIE xyY de 1931, on va pouvoir voir à quoi il sert.
Cet espace contient toutes les chrominances que l'oeil humain est capable de percevoir (on dit chrominance car on ne s'intéresse pas à l'intensité de la lumière, uniquement à sa couleur). Il peut donc servir à mettre en évidence les limitations des systèmes représentant des couleurs.
Voici quelques-uns de ces systèmes:
 On retrouve ici le CIE xyY sous le nom de "Horseshoes Shape of Visible Color", en français: "sabot de cheval des couleurs visibles", à cause de sa forme. Les quatre autres zone, triangulaires pour trois d'entre elles, représentent d'autres espaces colorimétriques.
On retrouve ici le CIE xyY sous le nom de "Horseshoes Shape of Visible Color", en français: "sabot de cheval des couleurs visibles", à cause de sa forme. Les quatre autres zone, triangulaires pour trois d'entre elles, représentent d'autres espaces colorimétriques.ProPhoto RGB, Adobe RGB et sRGB sont des systèmes de codages de la couleur utilisés en informatique. Nous en reparlerons plus en détails dans le post suivant au sujet du stockage numérique des images. Vous les avez peut-être aperçu comme paramètres de réglage si vous utilisez Photoshop. Ce diagramme permet de mettre en évidence leur limitations respectives. Par exemple, il est des couleurs qui seront codables en ProPhoto RBG, mais qu'il sera impossible de représenter en sRGB, un peu comme lorsque vous devez vous contenter d'une couleur approchante lorsque vous ne trouvez pas la teinte déjà passée dans un appartement dont vous voulez ne refaire qu'un seul mur.
La zone "2200 Matt Paper" est très intéressante car, contrairement aux trois autres qui correspondent à des systèmes de codage des couleurs, elle correspond à un phénomène physique tangible.
Savez-vous comment on fait pour donner une couleur à un objet? On y passe de la peinture bien sûr, mais on y dépose surtout des pigments qui vont absorber certaines longueurs d'ondes et en renvoyer d'autres. Comme la banane dont on a déjà parlé, les pigments de peinture modifient l'onde reçue pour en renvoyer une différente. Comme tous les rayonnements électro-magnétiques, les ondes sont périodiques et on peut les décomposer mathématiquement en une somme de sinusoïdes de différentes périodes (comme l'onde jaune bizarre qu'on a vu plus haut comme étant la somme des sinusoïdes verte et rouge). L'onde renvoyée par une surface sur laquelle on a appliqué des pigments peut donc être vue comme la somme d'un ensemble de sinusoïdes. Le phénomène physique de l'absorption fait que les pigments ne pourront que diminuer le nombre de sinusoïdes qui composent le rayonnement qu'ils vont réfléchir. De ce fait, on parle de synthèse soustractive de la couleur, car les pigments enlèvent des fréquences et ne peuvent en ajouter dans le rayonnement qu'ils renvoient.
Ainsi, en choisissant les pigments que l'on va déposer sur un objet ou une feuille, on peut produire différentes couleurs, mais pas autant que ce que l'oeil peut en percevoir. C'est ce que montre la zone appelée "2200 Matt Paper". Avec une impression sur papier glacé, il ne sera pas possible de reproduire toutes les couleurs que l'appareil photo aura pu saisir avec son capteur, car les couleurs obtenues sur le papier le sont par synthèse soustractive.
Autre remarque et pas des moindre à propos de ce diagramme CIE xyY coloré : l'écran de votre ordinateur, tout comme l'impression papier, possède ses propres limites dans l'affichage des couleurs. Elles sont d'ailleurs assez proche du système sRVB. Aussi, les couleurs que vous voyez dans ce diagramme en dehors de la zone sRVB ne sont que purement illustratives. Votre moniteur d'ordinateur, et les images JPG représentant ce diagramme, utilisent le système sRGB, il leur est par conséquent impossible de représenter les couleurs hors de cette zone. Pour cette raison, celles qui y sont affichées ne correspondent pas aux couleurs qui se trouvent réellement à cet endroit dans l'espace CIE xyY.
Si vous voulez constater vous même à quoi correspondent les limitations des appareils photo et des écrans LCD en matière de rendu des couleurs, il existe une expérience simple. Photographiez un coucher de soleil avec un appareil photo numérique, puis affichez immédiatement cette photo sur l'écran de de l'appareil et comparez les couleurs à celles du vrai coucher de soleil que vous avez encore devant vos yeux. Le résultat est saisissant. Si la plupart des couleurs que nous voyons tous les jours sont le fruit de la synthèse soustractive de la lumière (car tous les objets produisent leur couleur par synthèse soustractive), ce n'est pas le cas d'un coucher de soleil, qui nous envoi la lumière de notre étoile modifiée et filtrée par l'atmosphère terrestre. De ce fait, la plage des couleurs possible est incroyablement plus étendue, et les appareils photo, mais surtout les écrans LCD, sont alors incapables de restituer une telle gamme de couleurs.
Enfin, si vous voulez savoir si votre navigateur web gère correctement ces différents espaces colorimétriques, il y a cette page qui permet de faire un test très efficace pour le vérifier. L'image de droite est un repère, lorsque vous passez la souris dessus, quel que soit votre navigateur, les couleurs changent car l'espace colorimétrique utilisé change. La photo de gauche est le test : si ses couleurs changent lors vous passez la souris dessus (comme pour l'image de droite), c'est que votre navigateur ne gère pas correctement les espaces colorimétriques. Si c'est le cas, vous ne vous en êtes sans doute jamais rendu compte, mais cela veux dire que vous courez le risque d'avoir de fausses couleurs pour certaines photos des pages web, toutes celles qui ne sont pas codées dans l'espace sRGB en fait, car c'est celui utilisé par défaut par les navigateurs.
Luminosité, teinte et saturation (Lien)
Comme on vient de le voir, la représentation des couleurs est basée sur la réponse des cônes rouge, vert et bleu aux ondes électro-magnétiques. Ce modèle fonctionne, mais il présente le désavantage de ne pas mettre en évidence un paramètre fondamental de la lumière visible : la luminosité, ou plus exactement l'intensité du rayonnement.
Pour cette raison, un autre modèle de représentation des couleur est également très utilisé, le modèle HSL:
 Comme le modèle CIE xyY, le modèle HSL se base sur trois coordonnées (à cause des trois types de cônes, c'est inévitable). Cependant, au lieu d'associer chacune de ces coordonnées à la réponse en amplitude de chacun des cônes, une transformation mathématique est appliquée à chacune de ces trois amplitudes pour obtenir la luminosité (ou intensité lumineuse) comme l'une des trois coordonnées. Après cela, les deux autres coordonnées se déduisent logiquement car on a plus le choix si l'on veut pouvoir représenter toutes les couleurs visibles. À cause de l'effet de ces deux dernières coordonnées sur les couleurs, elles seront nommées Teinte (Hue en anglais) et Saturation.
Comme le modèle CIE xyY, le modèle HSL se base sur trois coordonnées (à cause des trois types de cônes, c'est inévitable). Cependant, au lieu d'associer chacune de ces coordonnées à la réponse en amplitude de chacun des cônes, une transformation mathématique est appliquée à chacune de ces trois amplitudes pour obtenir la luminosité (ou intensité lumineuse) comme l'une des trois coordonnées. Après cela, les deux autres coordonnées se déduisent logiquement car on a plus le choix si l'on veut pouvoir représenter toutes les couleurs visibles. À cause de l'effet de ces deux dernières coordonnées sur les couleurs, elles seront nommées Teinte (Hue en anglais) et Saturation.
La figure ci-dessus tente de représenter les couleurs dans ce modèle à trois dimensions. Notez cependant que dans l'espace CIE xyY en sabot de cheval que l'on a déjà vu, le fait d'avoir représenté les couleurs après division par la somme des trois composantes nous donnait en fait une vue de l'espace colorimétrique sans la luminosité. Ce sabot de cheval nous montrait un plan à luminosité fixe dans lequel les couleurs étaient réparties selon leur teinte et leur saturation. La saturation s'étendant du centre de couleur blanche (insaturée) vers l'extérieur, et la teinte variant sur tout le tour du sabot (selon les graduations de longueurs d'onde). C'est donc pour cette raison que l'on dit que l'impression papier (l'air "2200 Matt Paper") ne peut rendre les couleurs très saturées (celles se trouvant les bords du sabot).
Autre avantage historique de l'utilisation du système HSL, la compatibilité de la télévision couleur avec la télévision noir et blanc. Contrairement au passage de la télévision analogique à la télévision numérique qui crée une rupture totale dans la compatibilité des signaux, lorsque la télévision couleur a été introduite, le modèle HSL a été utilisé pour pouvoir "ajouter" la couleur par dessus le signal noir et blanc déjà émit (qui codait la luminosité). Ce deuxième signal a été modulé sur une autre onde porteuse et contenait la saturation et la teinte des pixels de chaque ligne de l'image. Ce couple de nouvelles coordonnées étaient alors appelé chominance. Ainsi, les signaux vidéo sont généralement codés de trois façons : composite, S-vidéo, ou RGB.
Comme on vient de le voir, la représentation des couleurs est basée sur la réponse des cônes rouge, vert et bleu aux ondes électro-magnétiques. Ce modèle fonctionne, mais il présente le désavantage de ne pas mettre en évidence un paramètre fondamental de la lumière visible : la luminosité, ou plus exactement l'intensité du rayonnement.
Pour cette raison, un autre modèle de représentation des couleur est également très utilisé, le modèle HSL:
 Comme le modèle CIE xyY, le modèle HSL se base sur trois coordonnées (à cause des trois types de cônes, c'est inévitable). Cependant, au lieu d'associer chacune de ces coordonnées à la réponse en amplitude de chacun des cônes, une transformation mathématique est appliquée à chacune de ces trois amplitudes pour obtenir la luminosité (ou intensité lumineuse) comme l'une des trois coordonnées. Après cela, les deux autres coordonnées se déduisent logiquement car on a plus le choix si l'on veut pouvoir représenter toutes les couleurs visibles. À cause de l'effet de ces deux dernières coordonnées sur les couleurs, elles seront nommées Teinte (Hue en anglais) et Saturation.
Comme le modèle CIE xyY, le modèle HSL se base sur trois coordonnées (à cause des trois types de cônes, c'est inévitable). Cependant, au lieu d'associer chacune de ces coordonnées à la réponse en amplitude de chacun des cônes, une transformation mathématique est appliquée à chacune de ces trois amplitudes pour obtenir la luminosité (ou intensité lumineuse) comme l'une des trois coordonnées. Après cela, les deux autres coordonnées se déduisent logiquement car on a plus le choix si l'on veut pouvoir représenter toutes les couleurs visibles. À cause de l'effet de ces deux dernières coordonnées sur les couleurs, elles seront nommées Teinte (Hue en anglais) et Saturation.La figure ci-dessus tente de représenter les couleurs dans ce modèle à trois dimensions. Notez cependant que dans l'espace CIE xyY en sabot de cheval que l'on a déjà vu, le fait d'avoir représenté les couleurs après division par la somme des trois composantes nous donnait en fait une vue de l'espace colorimétrique sans la luminosité. Ce sabot de cheval nous montrait un plan à luminosité fixe dans lequel les couleurs étaient réparties selon leur teinte et leur saturation. La saturation s'étendant du centre de couleur blanche (insaturée) vers l'extérieur, et la teinte variant sur tout le tour du sabot (selon les graduations de longueurs d'onde). C'est donc pour cette raison que l'on dit que l'impression papier (l'air "2200 Matt Paper") ne peut rendre les couleurs très saturées (celles se trouvant les bords du sabot).
Autre avantage historique de l'utilisation du système HSL, la compatibilité de la télévision couleur avec la télévision noir et blanc. Contrairement au passage de la télévision analogique à la télévision numérique qui crée une rupture totale dans la compatibilité des signaux, lorsque la télévision couleur a été introduite, le modèle HSL a été utilisé pour pouvoir "ajouter" la couleur par dessus le signal noir et blanc déjà émit (qui codait la luminosité). Ce deuxième signal a été modulé sur une autre onde porteuse et contenait la saturation et la teinte des pixels de chaque ligne de l'image. Ce couple de nouvelles coordonnées étaient alors appelé chominance. Ainsi, les signaux vidéo sont généralement codés de trois façons : composite, S-vidéo, ou RGB.
La balance des blancs (Lien)
Sources: Température de couleur, Pourpre.com, Wikipedia, Understanding White Balance
Avez-vous déjà essayé d'aller acheter un pot de peinture de la même couleur que celle qui couvre les trois autres murs de la pièce dont vous voulez refaire le quatrième?
Si ce n'est pas le cas, voici un bon exemple de la complexité de la perception de l'on a des couleurs:
Comme vous le constatez, l'impression que l'on a d'une couleur dépend d'un grand nombre de paramètres : nature et intensité de la lumière qui éclaire l'objet, couleurs environnant cet objet, et même parfois culture de l'observateur.
Voici deux autres exemples montant de façon spectaculaire la manière dont notre cerveau arrive à corriger notre perception des couleurs en fonction de l'environnement.
À votre avis, quelle est la couleur de la robe que l'on voit sur cette photo?
Blanche et or?
Certains diront bleu et noir.
Et bien ces derniers ont raison, leur cerveau a correctement corrigé les couleurs de cette photo. Car la lumière éclairant cette robe n'est pas blanche, ce qui fait que les couleurs sont faussées sur cette image. Vous pouvez le vérifier en téléchargeant l'image ci-dessus, puis en corrigeant le contraste et le luminosité. Vous verrez que le blanc est en fait un bleu très clair. Voici cette même robe photographiée avec une lumière blanche:
Bluffant n'est-ce pas?
Plus étonnant encore. Voici une image faite sur mesure pour tromper notre oeil. Croyez-le ou non, mais aucun des pixels de cette image, n'est rouge, tous sont de teinte cyan (sorte de bleu ciel) en représentation HSL.
Notre oeil voit du rouge là où il n'y en a pas car il corrige cette image, dans la mesure où il constate que tous les pixels sont de la même teinte (cyan), il interprète les différences de saturation et de luminosité en termes de couleurs des objets visibles.
Ainsi, la lumière reçue d'un objet ne permet pas de connaître la couleur de celui-ci. Les deux exemples ci-dessus illustre bien ce phénomène : sans information sur la lumière éclairant une scène, il est impossible de connaître la couleur des objets qui s'y trouvent. Le cerveau arrive à deviner cette couleur dans beaucoup de situation, mais pas toutes.
C'est pour qualifier la couleur des objets que l'on doit parler de la notion de balance des blancs.
L'exemple des carrés de couleur ci-dessus montre bien à quel point le cerveau interprète les couleurs en fonction de leur environnement. Regardez le T-shirt blanc de quelqu'un la nuit, à la lumière d'un réverbère. Vous le verrez blanc, alors qu'il vous renvoie la lumière du réverbère, qui est jaune orangée.
Comme les appareils numériques (hors mode automatique plus ou moins performant), ne sont pas capables d'une telle adaptation, il est nécessaire de les "calibrer" pour leur indiquer quelle est la couleur (au sens d'un point de l'espace CIE xyY) qui doit être considérée comme blanc. Le T-shirt sous le réverbère doit être considéré comme blanc malgrès la couleur jaune orangée qu'il renvoi, parce que notre cerveau s'adapte pour le voir blanc, l'appareil numérique (caméra ou appareil photo), devra lui aussi considérer "blanc" ce jaune orangé lorsqu'il codera sa couleur.
Dans le cas du réverbère la différence est flagrante, même à l'oeil nu, mais entre un soleil direct et un soleil voilé par des nuages, la couleur de la lumière ne sera pas la même, et il faudra là aussi re-calibrer l'appareil numérique, autrement dit corriger sa balance des blancs.
Dans les faits, ce calibrage consiste à indiquer à l'appareil photo quelle lumière doit être considérée comme blanche. En pratique, jusqu'à trois méthodes sont possibles. Elles sont généralement illustrées par une liste de pictogrammes semblable à celle-ci:
AWB signifie "Automatic White Balance", ou "Balance des Blancs Automatique" en français. Cette option existe pour simplifier l'usage de l'appareil photo pour un utilisateur non expérimenté. La méthode utilisée pour déterminer le point de l'espace colorimétrique qui doit être considéré comme blanc dépend de l'appareil. Il semble que chaque constructeur ait ses propres méthodes, plus ou moins élaborées en fonction de la puissance de calcul du processeur qui a été mis dans l'appareil. Ce qui est certain cependant, c'est que ces méthodes, si performantes soient-elles, ne pourront donner de bons résultats dans toutes les situations, et l'expertise du photographe sera toujours préférable.
La dernière option de cette liste n'est disponible que sur certains appareils, tels que les réflexes (SLR en anglais pour Single Lens Reflex). C'est la meilleure option, mais aussi la plus lourde à utiliser. Elle consiste à montrer à l'appareil quelle zone d'une image il doit considérer comme de couleur blanche. Selon les appareils, il faut soit photographier directement un objet blanc d'une taille suffisante pour occuper tout le centre de l'image, soit aller chercher dans la carte mémoire une photo ayant un objet blanc sur toute sa partie centrale. Cet objet blanc (une simple feuille par exemple) doit avoir été éclairé par la même source lumineuse que toutes les scènes que l'on va prendre en photo avec cette balance des blancs personnalisée. Ceci est parfois loin d'être évident. Comme je viens d'en parler, il suffit que le soleil se voile de nuages pour que la nature de la lumière change. La balance des blancs manuelle n'est donc intéressante que lorsqu'on prend des photos dans des conditions d'éclairement très stables (en intérieur avec la lumière artificielle fixe d'un théâtre ou d'une salle des fêtes par exemple).
Les autres options correspondent au modèle physique théorique des corps noirs. Ce modèle est utilisé car il correspond au phénomène physique à l'origine de l'émission lumineuse de la plupart des sources que l'on trouve dans la nature. L'idée à l'origine de ce modèle est que la matière, en fonction de sa température, émet un rayonnement électro-magnétique dont la longueur d'onde (la couleur), dépend de cette température. Il n'existe pas de matière réelle correspondant exactement au modèle théorique du corps noir, mais les parois intérieures d'un four s'en approchent. Plus le four sera chaud, plus le rayonnement qu'il va émettre sera énergétique et plus sa couleur sera décalée vers le bleu. Ce modèle permet donc d'associer une couleur à une température selon cette équivalence:
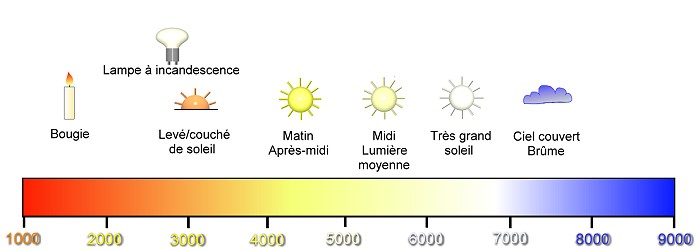
L'échelle en bas de ce diagramme est en degrés Kelvin (identiques aux Celsius à part le 0°K qui est situé à -273,15°C).
Comme vous le constatez, la couleur verte n'est pas présente sur cette échelle. C'est pour cette raison que le modèle des corps noirs n'est pas utilisable pour toutes les sources lumineuses, notamment pour les sources artificielles colorées ou pour une lumière indirecte reçue après réflexion sur un mur peint.
Pour cette raison, les options de balance des blancs "Lumière du jour", "Nuageux", "Ombre", "Incandescent", "Fluorescent" et "Flash" ne seront utilisables que dans les cas précis qu'elles décrivent. Cela représente cependant la majorité des situations de prise de vue.
Une remarque importante à propos de la balance des blancs : Et si la scène photographiée a plusieurs sources lumineuses de couleurs différentes?
Dans ce cas c'est plutôt compliqué.
Vous n'aurez pas cinquante solutions pour faire face à une telle situation :
Soit vous faites la photo au format RAW (on verra pourquoi dans le prochain post) et vous utilisez un logiciel pour traiter l'image afin d'avoir la bonne balance aux bons endroits. Ceci est faisable avec le couple Adobe Lightroom et Adobe Photoshop.
Soit vous choisissez une seule balance des blancs pour toute l'image sachant que certaines couleurs seront forcément différentes de la réalité, mais le résultat peut tout de même être artistiquement bon.
Dernière remarque enfin à propos de la balance des blancs : Pourquoi n'en était-il pas question en argentique?
En argentique, prendre une photo revient à rendre plus ou moins opaque aux différentes longueurs d'onde les différentes parties de la surface sensible. Cette réaction d'opacité va varier d'un film à l'autre, et le choix de la pellicule constituera un premier paramètre sur lequel le photographe pourra influer. Ensuite, la lumière utilisée lors de la reproduction de l'image, que ce soit une pellicule pour diapositives ou tirage papier (on dit réversible ou négatif), constituera elle aussi un paramètre influant sur le rendu des couleurs.
Voilà pourquoi on ne parlait pas de balance des blancs en argentique, car elle faisait partie du choix de la pellicule ainsi que de celui de l'appareil de projection pour écran ou tirage papier.
Le prochain post (et le dernier de cet atelier) parlera du stockage numérique des images et dira quelques mots sur les caractéristiques techniques d'un appareil photo numérique (nombre guide de flash, rôle du filtre passe bas du capteur...).
Sources: Température de couleur, Pourpre.com, Wikipedia, Understanding White Balance
Avez-vous déjà essayé d'aller acheter un pot de peinture de la même couleur que celle qui couvre les trois autres murs de la pièce dont vous voulez refaire le quatrième?
Si ce n'est pas le cas, voici un bon exemple de la complexité de la perception de l'on a des couleurs:
Comme vous le constatez, l'impression que l'on a d'une couleur dépend d'un grand nombre de paramètres : nature et intensité de la lumière qui éclaire l'objet, couleurs environnant cet objet, et même parfois culture de l'observateur.
Voici deux autres exemples montant de façon spectaculaire la manière dont notre cerveau arrive à corriger notre perception des couleurs en fonction de l'environnement.
À votre avis, quelle est la couleur de la robe que l'on voit sur cette photo?
Blanche et or?
Certains diront bleu et noir.
Et bien ces derniers ont raison, leur cerveau a correctement corrigé les couleurs de cette photo. Car la lumière éclairant cette robe n'est pas blanche, ce qui fait que les couleurs sont faussées sur cette image. Vous pouvez le vérifier en téléchargeant l'image ci-dessus, puis en corrigeant le contraste et le luminosité. Vous verrez que le blanc est en fait un bleu très clair. Voici cette même robe photographiée avec une lumière blanche:
Bluffant n'est-ce pas?
Plus étonnant encore. Voici une image faite sur mesure pour tromper notre oeil. Croyez-le ou non, mais aucun des pixels de cette image, n'est rouge, tous sont de teinte cyan (sorte de bleu ciel) en représentation HSL.
Notre oeil voit du rouge là où il n'y en a pas car il corrige cette image, dans la mesure où il constate que tous les pixels sont de la même teinte (cyan), il interprète les différences de saturation et de luminosité en termes de couleurs des objets visibles.
Ainsi, la lumière reçue d'un objet ne permet pas de connaître la couleur de celui-ci. Les deux exemples ci-dessus illustre bien ce phénomène : sans information sur la lumière éclairant une scène, il est impossible de connaître la couleur des objets qui s'y trouvent. Le cerveau arrive à deviner cette couleur dans beaucoup de situation, mais pas toutes.
C'est pour qualifier la couleur des objets que l'on doit parler de la notion de balance des blancs.
L'exemple des carrés de couleur ci-dessus montre bien à quel point le cerveau interprète les couleurs en fonction de leur environnement. Regardez le T-shirt blanc de quelqu'un la nuit, à la lumière d'un réverbère. Vous le verrez blanc, alors qu'il vous renvoie la lumière du réverbère, qui est jaune orangée.
Comme les appareils numériques (hors mode automatique plus ou moins performant), ne sont pas capables d'une telle adaptation, il est nécessaire de les "calibrer" pour leur indiquer quelle est la couleur (au sens d'un point de l'espace CIE xyY) qui doit être considérée comme blanc. Le T-shirt sous le réverbère doit être considéré comme blanc malgrès la couleur jaune orangée qu'il renvoi, parce que notre cerveau s'adapte pour le voir blanc, l'appareil numérique (caméra ou appareil photo), devra lui aussi considérer "blanc" ce jaune orangé lorsqu'il codera sa couleur.
Dans le cas du réverbère la différence est flagrante, même à l'oeil nu, mais entre un soleil direct et un soleil voilé par des nuages, la couleur de la lumière ne sera pas la même, et il faudra là aussi re-calibrer l'appareil numérique, autrement dit corriger sa balance des blancs.
Dans les faits, ce calibrage consiste à indiquer à l'appareil photo quelle lumière doit être considérée comme blanche. En pratique, jusqu'à trois méthodes sont possibles. Elles sont généralement illustrées par une liste de pictogrammes semblable à celle-ci:
AWB signifie "Automatic White Balance", ou "Balance des Blancs Automatique" en français. Cette option existe pour simplifier l'usage de l'appareil photo pour un utilisateur non expérimenté. La méthode utilisée pour déterminer le point de l'espace colorimétrique qui doit être considéré comme blanc dépend de l'appareil. Il semble que chaque constructeur ait ses propres méthodes, plus ou moins élaborées en fonction de la puissance de calcul du processeur qui a été mis dans l'appareil. Ce qui est certain cependant, c'est que ces méthodes, si performantes soient-elles, ne pourront donner de bons résultats dans toutes les situations, et l'expertise du photographe sera toujours préférable.
La dernière option de cette liste n'est disponible que sur certains appareils, tels que les réflexes (SLR en anglais pour Single Lens Reflex). C'est la meilleure option, mais aussi la plus lourde à utiliser. Elle consiste à montrer à l'appareil quelle zone d'une image il doit considérer comme de couleur blanche. Selon les appareils, il faut soit photographier directement un objet blanc d'une taille suffisante pour occuper tout le centre de l'image, soit aller chercher dans la carte mémoire une photo ayant un objet blanc sur toute sa partie centrale. Cet objet blanc (une simple feuille par exemple) doit avoir été éclairé par la même source lumineuse que toutes les scènes que l'on va prendre en photo avec cette balance des blancs personnalisée. Ceci est parfois loin d'être évident. Comme je viens d'en parler, il suffit que le soleil se voile de nuages pour que la nature de la lumière change. La balance des blancs manuelle n'est donc intéressante que lorsqu'on prend des photos dans des conditions d'éclairement très stables (en intérieur avec la lumière artificielle fixe d'un théâtre ou d'une salle des fêtes par exemple).
Les autres options correspondent au modèle physique théorique des corps noirs. Ce modèle est utilisé car il correspond au phénomène physique à l'origine de l'émission lumineuse de la plupart des sources que l'on trouve dans la nature. L'idée à l'origine de ce modèle est que la matière, en fonction de sa température, émet un rayonnement électro-magnétique dont la longueur d'onde (la couleur), dépend de cette température. Il n'existe pas de matière réelle correspondant exactement au modèle théorique du corps noir, mais les parois intérieures d'un four s'en approchent. Plus le four sera chaud, plus le rayonnement qu'il va émettre sera énergétique et plus sa couleur sera décalée vers le bleu. Ce modèle permet donc d'associer une couleur à une température selon cette équivalence:

L'échelle en bas de ce diagramme est en degrés Kelvin (identiques aux Celsius à part le 0°K qui est situé à -273,15°C).
Comme vous le constatez, la couleur verte n'est pas présente sur cette échelle. C'est pour cette raison que le modèle des corps noirs n'est pas utilisable pour toutes les sources lumineuses, notamment pour les sources artificielles colorées ou pour une lumière indirecte reçue après réflexion sur un mur peint.
Pour cette raison, les options de balance des blancs "Lumière du jour", "Nuageux", "Ombre", "Incandescent", "Fluorescent" et "Flash" ne seront utilisables que dans les cas précis qu'elles décrivent. Cela représente cependant la majorité des situations de prise de vue.
Une remarque importante à propos de la balance des blancs : Et si la scène photographiée a plusieurs sources lumineuses de couleurs différentes?
Dans ce cas c'est plutôt compliqué.
 |  |
|---|---|
| Balance des blanc sur la lumière de la lune | Balance des blanc sur la lumière de l'éclairage artificiel de la façade |
Vous n'aurez pas cinquante solutions pour faire face à une telle situation :
Soit vous faites la photo au format RAW (on verra pourquoi dans le prochain post) et vous utilisez un logiciel pour traiter l'image afin d'avoir la bonne balance aux bons endroits. Ceci est faisable avec le couple Adobe Lightroom et Adobe Photoshop.
Soit vous choisissez une seule balance des blancs pour toute l'image sachant que certaines couleurs seront forcément différentes de la réalité, mais le résultat peut tout de même être artistiquement bon.
Dernière remarque enfin à propos de la balance des blancs : Pourquoi n'en était-il pas question en argentique?
En argentique, prendre une photo revient à rendre plus ou moins opaque aux différentes longueurs d'onde les différentes parties de la surface sensible. Cette réaction d'opacité va varier d'un film à l'autre, et le choix de la pellicule constituera un premier paramètre sur lequel le photographe pourra influer. Ensuite, la lumière utilisée lors de la reproduction de l'image, que ce soit une pellicule pour diapositives ou tirage papier (on dit réversible ou négatif), constituera elle aussi un paramètre influant sur le rendu des couleurs.
Voilà pourquoi on ne parlait pas de balance des blancs en argentique, car elle faisait partie du choix de la pellicule ainsi que de celui de l'appareil de projection pour écran ou tirage papier.
Le prochain post (et le dernier de cet atelier) parlera du stockage numérique des images et dira quelques mots sur les caractéristiques techniques d'un appareil photo numérique (nombre guide de flash, rôle du filtre passe bas du capteur...).