Aspects non linaires des lentilles (Lien)
Sources: Distorsion (optique), from Wikipedia, Aberration géométrique, from Wikipedia
Aussi pédagogique et simple que soit l'optique géométrique, elle n'est pas en mesure de fournir une explication à certains phénomènes et certains défauts des lentilles optiques. Comme on a l'a vu, elle se limite à l'approximation de Gauss, il est donc intéressant de se pencher sur ce qui se passe lorsque celle-ci n'est plus valable.
Les différences entre le comportement des rayons lumineux en optique géométrique et dans la réalité peuvent être classées en différentes aberrations.
Sources: Distorsion (optique), from Wikipedia, Aberration géométrique, from Wikipedia
Aussi pédagogique et simple que soit l'optique géométrique, elle n'est pas en mesure de fournir une explication à certains phénomènes et certains défauts des lentilles optiques. Comme on a l'a vu, elle se limite à l'approximation de Gauss, il est donc intéressant de se pencher sur ce qui se passe lorsque celle-ci n'est plus valable.
Les différences entre le comportement des rayons lumineux en optique géométrique et dans la réalité peuvent être classées en différentes aberrations.
Aberration sphérique (Lien)
L'aberration sphérique est le premier aspect de la première des deux conséquences de l'erreur crée par l'approximation de Gauss. Cet aspect concerne les rayons incidents parallèles à l'axe optique.
Il est caractérisé par le fait que le point de convergence de rayons incidents parallèles n'est pas le même en fonction de l'endroit auquel ils traversent la lentille:
 Cette disparition du foyer (disparition par rapport à l'optique géométrique), crée un flou de l'image.
Cette disparition du foyer (disparition par rapport à l'optique géométrique), crée un flou de l'image.
L'aberration sphérique est le premier aspect de la première des deux conséquences de l'erreur crée par l'approximation de Gauss. Cet aspect concerne les rayons incidents parallèles à l'axe optique.
Il est caractérisé par le fait que le point de convergence de rayons incidents parallèles n'est pas le même en fonction de l'endroit auquel ils traversent la lentille:
 Cette disparition du foyer (disparition par rapport à l'optique géométrique), crée un flou de l'image.
Cette disparition du foyer (disparition par rapport à l'optique géométrique), crée un flou de l'image.
Aberration de coma (Lien)
L'aberration de coma est, avec l'aberration sphérique, le second aspect de la première conséquence de l'approximation de Gauss. L'appellation "aberration sphérique" était d'ailleurs autrefois utilisée pour qualifier ces deux aspects, on ne parlais pas alors d'aberration de coma.
C'est tout simplement la conséquence de la cause de l'aberration sphérique pour des rayons incidents non parallèles à l'axe optique.
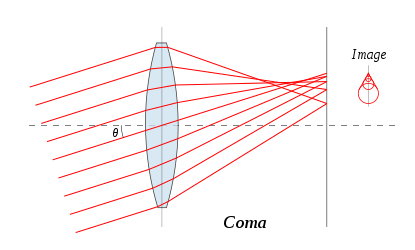 Comme pour l'aberration sphérique, la conséquence est la disparition du foyer et la création d'un flou de l'image.
Comme pour l'aberration sphérique, la conséquence est la disparition du foyer et la création d'un flou de l'image.
L'aberration de coma est, avec l'aberration sphérique, le second aspect de la première conséquence de l'approximation de Gauss. L'appellation "aberration sphérique" était d'ailleurs autrefois utilisée pour qualifier ces deux aspects, on ne parlais pas alors d'aberration de coma.
C'est tout simplement la conséquence de la cause de l'aberration sphérique pour des rayons incidents non parallèles à l'axe optique.
 Comme pour l'aberration sphérique, la conséquence est la disparition du foyer et la création d'un flou de l'image.
Comme pour l'aberration sphérique, la conséquence est la disparition du foyer et la création d'un flou de l'image.
Distorsion barillet, coussinet et vignetage (Lien)
Ces trois distorsions constituent la seconde conséquence de l'erreur crée par l'approximation de Gauss. Autrefois regroupés sous le nom de "courbure de champ", elles s'appliquent aux rayons incidents non parallèles (et se rejoignant pas au même point foyer en optique géométrique). De ce fait, ce ne sont pas des aberrations, mais des distorsions, car elles ne produisent pas de flou.
On l'a vu, plus l'angle d'incidence est grand, plus l'approximation de Gauss est fausse. La déviation des rayons incidents prévue par l'optique géométrique sera également de plus en plus fausse avec l'augmentation de l'angle de ces rayons. La conséquence est alors une déformation de l'image.
Comme on peut le voir sur la figure ci-dessous, cette déformation dépend de l'emplacement du diaphragme, cette paroi percée qui sert à limiter la quantité de lumière traversant la lentille (et par là même à augmenter la profondeur de champ).
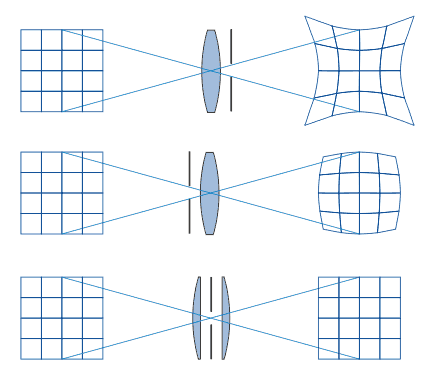
Si le diaphragme est placé avant la lentille, on obtient la distorsion de coussinet.
Si le diaphragme est placé après la lentille, on obtient la distorsion de barillet (souvent associé à du vignettage).
Comme on peut le voir sur le troisième schéma de l'illustration ci-dessus, l'utilisation d'une lentille supplémentaire permet d'annuler les distorsions de barillet et coussinet.
Alors que les distorsions de barillet et coussinet ne peuvent s'expliquer complètement qu'avec des calculs complexes, on peut avoir un aperçu de la cause du vignettage grâce au schéma ci-dessous:

La zone de l'image située dans l'axe du de l'ouverture du diaphragme reçoit le flux lumineux perpendiculairement à la surface sensible. De ce fait, un flux lumineux d'une section égale à la surface de l'ouverture du diaphragme illumine une zone la la surface sensible de la même surface.
En revanche, une zone de la même surface située sur le bord de l'image, plus loin de l'ouverture du diaphragme donc, recevra de celui-ci un flux lumineux moins large, et donc moins de lumière.
C'est pour cette simple raison géométrique que les bord d'un image sont vignettés. Sans optique corrective appropriée, ils reçoivent moins de lumière et sont donc plus sombre.
Petite anecdote enfin : si l'ancien terme donné à ces trois distorsions est "courbure de champ", c'est tout simplement parce que si la surface sensible sur laquelle se forme l'image était une portion de sphère, aucune de ces trois distorsions ne serait visible (mais les photos ne serait alors plus imprimées sur une surface plane mais sur un papier en forme de portion de sphère):

L'aberration sphérique ainsi que la courbure de champ peuvent être considérablement réduite par l'emploi de lentilles asphériques. Comme leur nom l'indique, elles n'ont pas la forme d'un portion de sphère mais comme génératrice une parabole. Ceci n'a malheureusement pas d'effet sur l'aberration chromatique.
Ces trois distorsions constituent la seconde conséquence de l'erreur crée par l'approximation de Gauss. Autrefois regroupés sous le nom de "courbure de champ", elles s'appliquent aux rayons incidents non parallèles (et se rejoignant pas au même point foyer en optique géométrique). De ce fait, ce ne sont pas des aberrations, mais des distorsions, car elles ne produisent pas de flou.
On l'a vu, plus l'angle d'incidence est grand, plus l'approximation de Gauss est fausse. La déviation des rayons incidents prévue par l'optique géométrique sera également de plus en plus fausse avec l'augmentation de l'angle de ces rayons. La conséquence est alors une déformation de l'image.
Comme on peut le voir sur la figure ci-dessous, cette déformation dépend de l'emplacement du diaphragme, cette paroi percée qui sert à limiter la quantité de lumière traversant la lentille (et par là même à augmenter la profondeur de champ).

 |  |
|---|---|
| Barillet avec vignettage | Coussinet |
Source: DxO Labs
Si le diaphragme est placé avant la lentille, on obtient la distorsion de coussinet.
Si le diaphragme est placé après la lentille, on obtient la distorsion de barillet (souvent associé à du vignettage).
Comme on peut le voir sur le troisième schéma de l'illustration ci-dessus, l'utilisation d'une lentille supplémentaire permet d'annuler les distorsions de barillet et coussinet.
Alors que les distorsions de barillet et coussinet ne peuvent s'expliquer complètement qu'avec des calculs complexes, on peut avoir un aperçu de la cause du vignettage grâce au schéma ci-dessous:

La zone de l'image située dans l'axe du de l'ouverture du diaphragme reçoit le flux lumineux perpendiculairement à la surface sensible. De ce fait, un flux lumineux d'une section égale à la surface de l'ouverture du diaphragme illumine une zone la la surface sensible de la même surface.
En revanche, une zone de la même surface située sur le bord de l'image, plus loin de l'ouverture du diaphragme donc, recevra de celui-ci un flux lumineux moins large, et donc moins de lumière.
C'est pour cette simple raison géométrique que les bord d'un image sont vignettés. Sans optique corrective appropriée, ils reçoivent moins de lumière et sont donc plus sombre.
Petite anecdote enfin : si l'ancien terme donné à ces trois distorsions est "courbure de champ", c'est tout simplement parce que si la surface sensible sur laquelle se forme l'image était une portion de sphère, aucune de ces trois distorsions ne serait visible (mais les photos ne serait alors plus imprimées sur une surface plane mais sur un papier en forme de portion de sphère):

L'aberration sphérique ainsi que la courbure de champ peuvent être considérablement réduite par l'emploi de lentilles asphériques. Comme leur nom l'indique, elles n'ont pas la forme d'un portion de sphère mais comme génératrice une parabole. Ceci n'a malheureusement pas d'effet sur l'aberration chromatique.
Aberration chromatique (Lien)
Source: DxO Labs
L'aberration chromatique concerne, comme son nom l'indique, un comportement différent en fonction de la couleur de la lumière (sa longueur d'onde). C'est en quelque sorte une surcouche aux deux aberrations déjà vu car son origine vient de la déviation différente que la lentille fait subir aux rayons lumineux en fonction de leur longueur d'onde.
Au regard de la figure ci-dessous, on aurait put croire que ni l'aberration sphérique, ni l'aberration de coma n'aurai pu empêcher ces deux rayons parallèles à l'axe optique et traversant la lentille à la même distance du foyer de converger en un même point, mais il n'en est rien. Chaque longueur d'onde du rayon lumineux est dévié de façon légèrement différente.
La conséquence de cette aberration est également un flou, mais avec cette fois une variation de la couleur (l'intérieur du C ci-dessus est plutôt bleu, et l'extérieur jaune).
Source: DxO Labs
L'aberration chromatique concerne, comme son nom l'indique, un comportement différent en fonction de la couleur de la lumière (sa longueur d'onde). C'est en quelque sorte une surcouche aux deux aberrations déjà vu car son origine vient de la déviation différente que la lentille fait subir aux rayons lumineux en fonction de leur longueur d'onde.
Au regard de la figure ci-dessous, on aurait put croire que ni l'aberration sphérique, ni l'aberration de coma n'aurai pu empêcher ces deux rayons parallèles à l'axe optique et traversant la lentille à la même distance du foyer de converger en un même point, mais il n'en est rien. Chaque longueur d'onde du rayon lumineux est dévié de façon légèrement différente.
 |  |
|---|
Astigmatisme (Lien)
L'astigmatisme, contrairement aux quatre autres aberrations dont on vient de parler, ne provient pas de l'approximation de Gauss, mais de la limitation de notre connaissance des conditions réelles.
Dans tous les modèles mathématiques des lentilles, celles-ci sont considérées comme ayant une symétrie axiale. Dans la réalité, ils est impossible de fabriquer une lentille avec une symétrie parfaite. Les défauts de fabrication sont ainsi à l'origine d'un comportement des rayons lumineux différent du modèle mathématique, et cela crée une source de flou supplémentaire.
L'astigmatisme, contrairement aux quatre autres aberrations dont on vient de parler, ne provient pas de l'approximation de Gauss, mais de la limitation de notre connaissance des conditions réelles.
Dans tous les modèles mathématiques des lentilles, celles-ci sont considérées comme ayant une symétrie axiale. Dans la réalité, ils est impossible de fabriquer une lentille avec une symétrie parfaite. Les défauts de fabrication sont ainsi à l'origine d'un comportement des rayons lumineux différent du modèle mathématique, et cela crée une source de flou supplémentaire.
L'expostion, paramètre clé de la photographie (Lien)
On l'a vu au début de la partie 3, photographier c'est écrire avec la lumière. Comme on choisi ses crayons et son papier lorsqu'on fait un dessin, on va choisir sa lumière et sa surface sensible lorsqu'on photographie.
C'était vrai avec le surfaces argentiques et ça l'est encore avec les capteurs électroniques : l'image fixée va dépendre de la quantité de lumière reçue et de la surface qui le fixe. Avec l'argentique, en fonction de la taille des gains de l'émulsion d'agent, ceux-ci pouvait noircir plus ou moins vite pour une même quantité de lumière. Pour les capteurs électroniques, la tension qu'ils délivre pourra être différent avec la même quantité de lumière en fonction du circuit électronique qui conditionnera son signal et son alimentation.
Si l'on ne maîtrise pas la façon dont la lumière va modifier la surface sensible, on obtiendra soit des images toute blanches, soit des images toutes noires. Pour cette raison, différentes techniques et systèmes on été mis au point pour maîtriser au mieux l'effet de la lumière sur la surface sensible.
On l'a vu au début de la partie 3, photographier c'est écrire avec la lumière. Comme on choisi ses crayons et son papier lorsqu'on fait un dessin, on va choisir sa lumière et sa surface sensible lorsqu'on photographie.
C'était vrai avec le surfaces argentiques et ça l'est encore avec les capteurs électroniques : l'image fixée va dépendre de la quantité de lumière reçue et de la surface qui le fixe. Avec l'argentique, en fonction de la taille des gains de l'émulsion d'agent, ceux-ci pouvait noircir plus ou moins vite pour une même quantité de lumière. Pour les capteurs électroniques, la tension qu'ils délivre pourra être différent avec la même quantité de lumière en fonction du circuit électronique qui conditionnera son signal et son alimentation.
Si l'on ne maîtrise pas la façon dont la lumière va modifier la surface sensible, on obtiendra soit des images toute blanches, soit des images toutes noires. Pour cette raison, différentes techniques et systèmes on été mis au point pour maîtriser au mieux l'effet de la lumière sur la surface sensible.
La sensibilité ISO (Lien)
Source: Wikipedia
La sensibilité ISO est la caractérisation de la sensibilité à la lumière d'une surface sensible. Historiquement, trois échelles sont utilisées : ISO, ASA et DIN, mais elles sont équivalentes dans la mesure où la conversion d'une échelle à une autre est simple.
Les nombre ISO et ASA sont égaux, et l'échelle DIN peut se convertir en ISO de la façon suivante : DIN = 10 log ISO + 1, et par conséquent ISO = 10 ^ ( (DIN - 1)/10 ).
Par exemple : 100ISO = 10 log 100 + 1 = 10 * 2 + 1 = 21°DIN.
Même si la méthode de détermination du nombre ISO change radicalement entre argentique et numérique, son utilisation par le photographe est identique.
L'échelle de sensibilité DIN est une échelle logarithmique.
La bonne compréhension de ce qu'est une échelle logarithmique est capitale pour tout ce qui va suivre, donc nous allons nous y attarder.
Pour étudier certains phénomènes physiques, il est nécessaire de s'intéresser aux variations et non aux grandeurs absolues.
Pour prendre un exemple qui parlera à tout le monde, imaginez que vous deviez parcourir 1km à pied. Cela ne pose pas de problème. Si en arrivant vous vous apercevez que vous vous êtes trompé et que votre destination est en fait à 2km, vous risque d'être contrarié.
Imaginez maintenant que vous deviez parcourir 100km en voiture. Si en arrivant vous vous apercevez que votre point d'arrivé est en fait à 101km, c'est tout juste si vous vous en rendrez compte.
L'échelle logarithmique est faite pour illustrer de façon la plus évidente possible cette notion de relativité. Un kilomètre peut représenter beaucoup ou très peu, tout dépend du contexte. Cependant, si on vous avait dit que votre trajet à pied serait prolongé de 100% et que votre trajet en voiture le serait de 1%, la différence aurait été évidente, bien que dans les deux cas il s'agisse d'un seul kilomètre de chemin supplémentaire.
De la même façon, si vous avez à parcourir 1km, 10km, 100km ou 10 000km, vous n'utiliserez pas le même moyen de transport. Peu importe la distance exacte, ce qui vous importe réellement c'est le nombre de zéros (un peu comme un gagnant du loto).
L'échelle logarithmique est justement faite pour représenter le nombre de zéro d'une grandeur, sans se soucier des chiffres peu significatifs.
Pour passer une grandeur de l'échelle normale (dite linéaire) à l'échelle logarithmique, il faut transformer chaque valeur d'abscisse (les distances en kilomètres par exemple) en une puissance de dix. Ainsi, on pourra visualiser au niveau du chiffre 3 ce qui se passe autour de 1000 (trois zéros), au niveau de 4 se qui se passe autour de 10000 (quatre zéros), et ainsi de suite.
Avec la lumière (et, soit dit en passant, les sons), les phénomènes se passent sur le même type d'échelle que notre parcours en kilomètres. Comme on l'a vu dans un post précédent, notre oeil est capable de voir la nuit comme en plein soleil, lorsque la quantité de lumière est mille milliards de fois supérieure (12 zéros, soit la différence entre l'étoile de plus faible magnitude visible à l'oeil nu et une plage de sable blanc en plein soleil un jour d'été à midi). (Sources: Magnitude apparente, from Wikipedia, Lux unit, from Wikipedia)
À cause de ce rapport colossal, certaines grandeurs utilisées en photographie se mesurent sur une échelle logarithmique. Peu importe les valeurs absolues, seules comptent les variations.
Ainsi, l'échelle ISO (bien que non logarithmique) est purement arbitraire. On n'essayera pas de montrer le rapport entre le nombre ISO et la mesure de luminosité, on va en revanche apprendre à appréhender les effets d'un changement de ce nombre.
Par convention, le point de repère est la valeur 100ISO, un peu comme celui de l'échelle de température Celsius est 100°C pour l'ébullition de l'eau pure à pression atmosphérique. Pour l'argentique, 100ISO était l'une des sensibilités les plus utilisées, et pour le numérique il se trouve que c'est celle à laquelle les capteurs procurent la meilleure qualité d'image (voir liens au début de la partie 2 de cet atelier).
L'échelle logarithmique dont on vient de parler intervient sur la sensibilité lorsqu'on utilise l'échelle DIN, ce qui est cependant assez rare. Multiplier par 10 la sensibilité d'une surface reviendra à multiplier par 10 l'ISO, de 100 à 1000 par exemple, mais ajouter 10 au DIN, de 21° à 31°.
Ce qui est le plus important à savoir pour choisir sa sensibilité ISO est l'influence sur la qualité de l'image.
En argentique, les grains captant la lumière étaient plus gros lorsque la sensibilité augmentait (lorsque l'ISO augmentait). Ainsi, les pellicules noir et blanc 3200ISO étaient connues pour leur grain particulier:
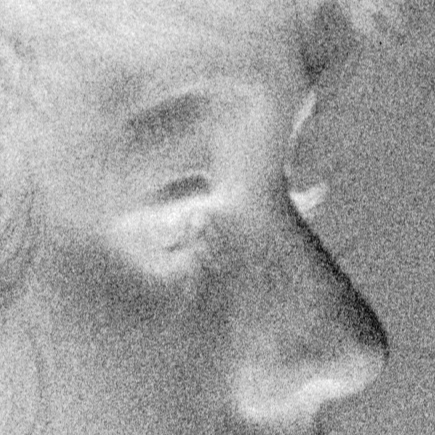 Source: Wikipedia
Source: Wikipedia
En numérique, l'augmentation de l'ISO améliore la sensibilité en même temps que le bruit. Le bruit? En photographie?
Oui, comme le capteur de l'appareil photo transforme la lumière en signal électrique, celui-ci peut contenir du bruit, comme le son d'un violon peut être mélangé au bruit ambiant lorsqu'il arrive à vos oreilles.
Sur l'image, cela se traduit par des pixels qui n'ont pas la bonne couleur.
Mis à part le bruit, quel est l'influence du changement de la sensibilité?
Pas grand chose, si ce n'est l'exposition du cliché bien sûr. Pour bien comprendre cela, nous allons d'abord parler des autres paramètres qui peuvent influer sur l'exposition, et nous reviendrons à l'ISO ensuite.
Source: Wikipedia
La sensibilité ISO est la caractérisation de la sensibilité à la lumière d'une surface sensible. Historiquement, trois échelles sont utilisées : ISO, ASA et DIN, mais elles sont équivalentes dans la mesure où la conversion d'une échelle à une autre est simple.
Les nombre ISO et ASA sont égaux, et l'échelle DIN peut se convertir en ISO de la façon suivante : DIN = 10 log ISO + 1, et par conséquent ISO = 10 ^ ( (DIN - 1)/10 ).
Par exemple : 100ISO = 10 log 100 + 1 = 10 * 2 + 1 = 21°DIN.
Même si la méthode de détermination du nombre ISO change radicalement entre argentique et numérique, son utilisation par le photographe est identique.
L'échelle de sensibilité DIN est une échelle logarithmique.
La bonne compréhension de ce qu'est une échelle logarithmique est capitale pour tout ce qui va suivre, donc nous allons nous y attarder.
Pour étudier certains phénomènes physiques, il est nécessaire de s'intéresser aux variations et non aux grandeurs absolues.
Pour prendre un exemple qui parlera à tout le monde, imaginez que vous deviez parcourir 1km à pied. Cela ne pose pas de problème. Si en arrivant vous vous apercevez que vous vous êtes trompé et que votre destination est en fait à 2km, vous risque d'être contrarié.
Imaginez maintenant que vous deviez parcourir 100km en voiture. Si en arrivant vous vous apercevez que votre point d'arrivé est en fait à 101km, c'est tout juste si vous vous en rendrez compte.
L'échelle logarithmique est faite pour illustrer de façon la plus évidente possible cette notion de relativité. Un kilomètre peut représenter beaucoup ou très peu, tout dépend du contexte. Cependant, si on vous avait dit que votre trajet à pied serait prolongé de 100% et que votre trajet en voiture le serait de 1%, la différence aurait été évidente, bien que dans les deux cas il s'agisse d'un seul kilomètre de chemin supplémentaire.
De la même façon, si vous avez à parcourir 1km, 10km, 100km ou 10 000km, vous n'utiliserez pas le même moyen de transport. Peu importe la distance exacte, ce qui vous importe réellement c'est le nombre de zéros (un peu comme un gagnant du loto).
L'échelle logarithmique est justement faite pour représenter le nombre de zéro d'une grandeur, sans se soucier des chiffres peu significatifs.
Pour passer une grandeur de l'échelle normale (dite linéaire) à l'échelle logarithmique, il faut transformer chaque valeur d'abscisse (les distances en kilomètres par exemple) en une puissance de dix. Ainsi, on pourra visualiser au niveau du chiffre 3 ce qui se passe autour de 1000 (trois zéros), au niveau de 4 se qui se passe autour de 10000 (quatre zéros), et ainsi de suite.
Avec la lumière (et, soit dit en passant, les sons), les phénomènes se passent sur le même type d'échelle que notre parcours en kilomètres. Comme on l'a vu dans un post précédent, notre oeil est capable de voir la nuit comme en plein soleil, lorsque la quantité de lumière est mille milliards de fois supérieure (12 zéros, soit la différence entre l'étoile de plus faible magnitude visible à l'oeil nu et une plage de sable blanc en plein soleil un jour d'été à midi). (Sources: Magnitude apparente, from Wikipedia, Lux unit, from Wikipedia)
À cause de ce rapport colossal, certaines grandeurs utilisées en photographie se mesurent sur une échelle logarithmique. Peu importe les valeurs absolues, seules comptent les variations.
Ainsi, l'échelle ISO (bien que non logarithmique) est purement arbitraire. On n'essayera pas de montrer le rapport entre le nombre ISO et la mesure de luminosité, on va en revanche apprendre à appréhender les effets d'un changement de ce nombre.
Par convention, le point de repère est la valeur 100ISO, un peu comme celui de l'échelle de température Celsius est 100°C pour l'ébullition de l'eau pure à pression atmosphérique. Pour l'argentique, 100ISO était l'une des sensibilités les plus utilisées, et pour le numérique il se trouve que c'est celle à laquelle les capteurs procurent la meilleure qualité d'image (voir liens au début de la partie 2 de cet atelier).
L'échelle logarithmique dont on vient de parler intervient sur la sensibilité lorsqu'on utilise l'échelle DIN, ce qui est cependant assez rare. Multiplier par 10 la sensibilité d'une surface reviendra à multiplier par 10 l'ISO, de 100 à 1000 par exemple, mais ajouter 10 au DIN, de 21° à 31°.
Ce qui est le plus important à savoir pour choisir sa sensibilité ISO est l'influence sur la qualité de l'image.
En argentique, les grains captant la lumière étaient plus gros lorsque la sensibilité augmentait (lorsque l'ISO augmentait). Ainsi, les pellicules noir et blanc 3200ISO étaient connues pour leur grain particulier:
 Source: Wikipedia
Source: WikipediaEn numérique, l'augmentation de l'ISO améliore la sensibilité en même temps que le bruit. Le bruit? En photographie?
Oui, comme le capteur de l'appareil photo transforme la lumière en signal électrique, celui-ci peut contenir du bruit, comme le son d'un violon peut être mélangé au bruit ambiant lorsqu'il arrive à vos oreilles.
Sur l'image, cela se traduit par des pixels qui n'ont pas la bonne couleur.
Source: Focus numerique
Mis à part le bruit, quel est l'influence du changement de la sensibilité?
Pas grand chose, si ce n'est l'exposition du cliché bien sûr. Pour bien comprendre cela, nous allons d'abord parler des autres paramètres qui peuvent influer sur l'exposition, et nous reviendrons à l'ISO ensuite.
Le nombre d'ouverture (Lien)
Source: Wikipedia
On l'a vu avec la chambre noire, si on souhaite plus de lumière, il faut augmenter la taille du trou. Et quand on utilise une lentille, il faut augmenter sa taille (ou le trou de la paroi qu'on a placé devant ou derrière elle).
On vient de voir que l'ISO est une échelle arbitraire, qu'en est-il pour la taille du trou laissant passer la lumière?
Avec une lentille, l'image produite bénéficie d'un grossissement qui dépend de la focale de cette lentille (on l'a vu dans un post précédent). Ainsi, pour un trou de taille fixe, on aura moins de lumière si la focale augmente, puisque la taille de la surface sensible, elle, ne changera pas. C'est logique, si j'essaie d'éclairer la page d'un livre avec une lampe de poche, ça sera efficace, mais si j'essaie d'éclairer une pièce entière, j'y verrai beaucoup moins bien. C'est le même principe avec la focale et la taille du trou.
Afin de définir une échelle qui ne dépende pas de la focale, on ne parlera pas de taille de trou mais de nombre d'ouverture. Comment créer une valeur indépendante de la focale tout en dépendant de la taille du trou laissant la lumière traverser la lentille? En divisant tout simplement la taille de ce trou par la distance focale de la lentille qui lui est associée.
Ainsi le nombre d'ouverture correspond tout simplement à la focale divisée par le diamètre de ce qu'on appelle la "pupille d'entrée". La pupille d'entrée correspond à la zone circulaire maximum au travers de laquelle la lumière peut traverser la totalité de la lentille (ou de l'objectif) pour atteindre la surface sensible. Sa taille dépend de la taille des lentilles mais aussi, lorsque l'on veut moins de lumière, de la taille du trou qui leur est associé. Ce trou est de taille variable dans la plupart des objectifs (car il n'est pas modifiable sur les appareils jetables et les téléphones portables). Un mécanisme ingénieux basé sur des lamelles glissant les unes sur les autres permet d'obtenir un trou de taille variable dont le diamètre peut être commandé électriquement. Voici une vue de détail de cette mécanique:
 Source: Blog Mamiya C
Source: Blog Mamiya C
Pour un objectif de 50mm de focale avec une pupille d'entrée de 35mm de diamètre, le nombre d'ouverture sera de 50 / 35 = 1,43. Ce nombre ne correspond pas au diamètre de la pupille divisée par la focale pour une simple raison de commodité. En inversant le sens de la division, on obtient une échelle qui va des environs de 1 aux alentours de 32 au lieu d'aller de 1 vers 0,031.
Le nombre d'ouverture représente donc, indépendamment de la focale, la quantité de lumière que laisser passer l'objectif. On le note généralement F/x ou 1/x, x étant le nombre lui même. Cela donne habituellement des ouvertures notées par exemple f/5.6, f1.4...
Afin d'être tout à fait complet (et le plus exact possible), il faut apporter une petite précision à la phrase précédente. Le nombre d'ouverture ne donne pas exactement la quantité de lumière que laisse passer l'objectif. En effet, si les lentilles sont toutes sales, le nombre d'ouverture n'aura pas changé, mais beaucoup moins de lumière pourra traverser l'objectif. Pour cette raison, il peut être intéressant de se renseigner également sur le "Transmittance" de l'objectif. Les lentilles d'un objectif, comme tout objet en verre, laissent une partie de la lumière les traverser, et en réfléchissent une autre (il y a toujours des reflets sur une vitre, même si on peut voir à travers). Ainsi, chaque lentille d'un objectif va renvoyer une partie de la lumière au lieu de la laisser la traverser, et celle-ci sera perdu pour la surface sensible. C'est pour cette raison que les lentilles sont traitées avec un anti-reflet qui leur donne ces couleurs particulières, mais en fonction du nombre qu'en compte un objectif, celui-ci, malgré son nombre d'ouverture, pourra laisser passer plus ou moins de lumière qu'un autre modèle avec la même focale et le même nombre d'ouverture. Typiquement, les zooms ont une transmittance moindre que les focales fixes car ils comportent plus de lentilles.
Mise à part l'exposition du cliché, quels sont les effets des grandes et faibles ouvertures du diaphragme?
Si vous vous souvenez de la partie sur les aberrations, vous aurez compris que les grandes ouvertures (proche de f1) font entrer des rayons à des angles d'incidence qui les éloignent des conditions de Gauss, ce qui augmente l'effet des aberrations sphériques, chromatiques ainsi que la courbure de champ.
Dans ce cas on doit toujours utiliser la plus petite ouverture possible?
Non plus. La lumière se comportant comme une onde, elle se diffracte lorsqu'elle traverse une ouverture. (Source: Diffraction, from Wikipedia)
Un peu à la manière de ces vagues qui arrivent parallèles et se mettent à former des cercles après avoir traversé le chenal.
Le phénomène de diffraction de la lumière à travers un trou circulaire (comme le diaphragme) crée l'image d'un tâche entourée de cercles concentrique au lieu de donner l'image d'un point net.
Le taille de cette tâche a été caractérisée par Joseph von Fraunhofer, elle est égale à 1,22λf/ d. (Sources: Théorie de la diffraction, from Wikipedia, Joseph von Fraunhofer, from Wikipedia)
Le terme λ est le longueur d'onde de la lumière qui traverse le trou.
Le terme f est la focale de l'optique qui crée l'image du trou (car la diffraction de Fraunhofer caractérise la limite de résolution des instruments optiques, bien qu'il n'est pas nécessaire d'associer une lentille à un trou pour obtenir un phénomène de diffraction).
Le terme d est le diamètre du trou.
Cette formule nous montre que plus le trou sera grand, moins la tâche de diffraction sera grande. On constate aussi que le phénomène de diffraction augmente avec la focale et la longueur d'onde (le rouge est plus diffractés que le bleu).
Pour toutes ces raisons, on évitera d'utiliser des trop grandes et de de trop petites ouvertures. Par exemple, dans le cas de mes objectifs (17-55mm f/2.8, 70-200mm f/2.8 et 10mm f/2.8), les tests de résolution réalisés par le laboratoire DxO montrent qu'il est préférable d'utiliser les ouvertures entre f/5.6 et f/8 pour une meilleure qualité d'image.
En règle générale, les meilleures résolutions des objectifs sont obtenues avec des ouvertures entre f/4 et f/11 selon les modèles.
Source: Wikipedia
On l'a vu avec la chambre noire, si on souhaite plus de lumière, il faut augmenter la taille du trou. Et quand on utilise une lentille, il faut augmenter sa taille (ou le trou de la paroi qu'on a placé devant ou derrière elle).
On vient de voir que l'ISO est une échelle arbitraire, qu'en est-il pour la taille du trou laissant passer la lumière?
Avec une lentille, l'image produite bénéficie d'un grossissement qui dépend de la focale de cette lentille (on l'a vu dans un post précédent). Ainsi, pour un trou de taille fixe, on aura moins de lumière si la focale augmente, puisque la taille de la surface sensible, elle, ne changera pas. C'est logique, si j'essaie d'éclairer la page d'un livre avec une lampe de poche, ça sera efficace, mais si j'essaie d'éclairer une pièce entière, j'y verrai beaucoup moins bien. C'est le même principe avec la focale et la taille du trou.
Afin de définir une échelle qui ne dépende pas de la focale, on ne parlera pas de taille de trou mais de nombre d'ouverture. Comment créer une valeur indépendante de la focale tout en dépendant de la taille du trou laissant la lumière traverser la lentille? En divisant tout simplement la taille de ce trou par la distance focale de la lentille qui lui est associée.
Ainsi le nombre d'ouverture correspond tout simplement à la focale divisée par le diamètre de ce qu'on appelle la "pupille d'entrée". La pupille d'entrée correspond à la zone circulaire maximum au travers de laquelle la lumière peut traverser la totalité de la lentille (ou de l'objectif) pour atteindre la surface sensible. Sa taille dépend de la taille des lentilles mais aussi, lorsque l'on veut moins de lumière, de la taille du trou qui leur est associé. Ce trou est de taille variable dans la plupart des objectifs (car il n'est pas modifiable sur les appareils jetables et les téléphones portables). Un mécanisme ingénieux basé sur des lamelles glissant les unes sur les autres permet d'obtenir un trou de taille variable dont le diamètre peut être commandé électriquement. Voici une vue de détail de cette mécanique:
 Source: Blog Mamiya C
Source: Blog Mamiya CPour un objectif de 50mm de focale avec une pupille d'entrée de 35mm de diamètre, le nombre d'ouverture sera de 50 / 35 = 1,43. Ce nombre ne correspond pas au diamètre de la pupille divisée par la focale pour une simple raison de commodité. En inversant le sens de la division, on obtient une échelle qui va des environs de 1 aux alentours de 32 au lieu d'aller de 1 vers 0,031.
Le nombre d'ouverture représente donc, indépendamment de la focale, la quantité de lumière que laisser passer l'objectif. On le note généralement F/x ou 1/x, x étant le nombre lui même. Cela donne habituellement des ouvertures notées par exemple f/5.6, f1.4...
Afin d'être tout à fait complet (et le plus exact possible), il faut apporter une petite précision à la phrase précédente. Le nombre d'ouverture ne donne pas exactement la quantité de lumière que laisse passer l'objectif. En effet, si les lentilles sont toutes sales, le nombre d'ouverture n'aura pas changé, mais beaucoup moins de lumière pourra traverser l'objectif. Pour cette raison, il peut être intéressant de se renseigner également sur le "Transmittance" de l'objectif. Les lentilles d'un objectif, comme tout objet en verre, laissent une partie de la lumière les traverser, et en réfléchissent une autre (il y a toujours des reflets sur une vitre, même si on peut voir à travers). Ainsi, chaque lentille d'un objectif va renvoyer une partie de la lumière au lieu de la laisser la traverser, et celle-ci sera perdu pour la surface sensible. C'est pour cette raison que les lentilles sont traitées avec un anti-reflet qui leur donne ces couleurs particulières, mais en fonction du nombre qu'en compte un objectif, celui-ci, malgré son nombre d'ouverture, pourra laisser passer plus ou moins de lumière qu'un autre modèle avec la même focale et le même nombre d'ouverture. Typiquement, les zooms ont une transmittance moindre que les focales fixes car ils comportent plus de lentilles.
Mise à part l'exposition du cliché, quels sont les effets des grandes et faibles ouvertures du diaphragme?
Si vous vous souvenez de la partie sur les aberrations, vous aurez compris que les grandes ouvertures (proche de f1) font entrer des rayons à des angles d'incidence qui les éloignent des conditions de Gauss, ce qui augmente l'effet des aberrations sphériques, chromatiques ainsi que la courbure de champ.
Dans ce cas on doit toujours utiliser la plus petite ouverture possible?
Non plus. La lumière se comportant comme une onde, elle se diffracte lorsqu'elle traverse une ouverture. (Source: Diffraction, from Wikipedia)
Un peu à la manière de ces vagues qui arrivent parallèles et se mettent à former des cercles après avoir traversé le chenal.
Source: Site web de F.Gély
Le phénomène de diffraction de la lumière à travers un trou circulaire (comme le diaphragme) crée l'image d'un tâche entourée de cercles concentrique au lieu de donner l'image d'un point net.
Le taille de cette tâche a été caractérisée par Joseph von Fraunhofer, elle est égale à 1,22λf/ d. (Sources: Théorie de la diffraction, from Wikipedia, Joseph von Fraunhofer, from Wikipedia)
Le terme λ est le longueur d'onde de la lumière qui traverse le trou.
Le terme f est la focale de l'optique qui crée l'image du trou (car la diffraction de Fraunhofer caractérise la limite de résolution des instruments optiques, bien qu'il n'est pas nécessaire d'associer une lentille à un trou pour obtenir un phénomène de diffraction).
Le terme d est le diamètre du trou.
Cette formule nous montre que plus le trou sera grand, moins la tâche de diffraction sera grande. On constate aussi que le phénomène de diffraction augmente avec la focale et la longueur d'onde (le rouge est plus diffractés que le bleu).
Pour toutes ces raisons, on évitera d'utiliser des trop grandes et de de trop petites ouvertures. Par exemple, dans le cas de mes objectifs (17-55mm f/2.8, 70-200mm f/2.8 et 10mm f/2.8), les tests de résolution réalisés par le laboratoire DxO montrent qu'il est préférable d'utiliser les ouvertures entre f/5.6 et f/8 pour une meilleure qualité d'image.
En règle générale, les meilleures résolutions des objectifs sont obtenues avec des ouvertures entre f/4 et f/11 selon les modèles.
Indice de lumination (Lien)
Sources: Indice de lumination, from Wikipedia, Candela, from Wikipedia, Cours de Sandra Fiori, université de Montpellier
Faire de la photographie c'est écrire avec de la lumière, il semble donc naturel de pouvoir quantifier cette lumière. Pour cela, il est d'abord nécessaire de comprendre les différents concepts mis en jeux. Pour cela nous allons utiliser l'analogie hydraulique (encore elle).
Une source lumineuse émet de la lumière un peu comme un système d'arrosage émet de l'eau. On peut donc caractériser cette source par la quantité d'eau qu'elle émet, son intensité. Pour l'arrosage ça sera des litres par seconde, et pour la lumière des candela. Mais pourquoi n'utilise-t-on pas des truc par seconde dans le cas de la lumière? Parce que la lumière se comporte un peu comme une onde (comme des vagues ou un son) et un peu comme des particules (comme un jet d'eau). Donc il est impossible de la quantifier de la même façon que de l'eau. Il a donc été décidé de caractériser les sources lumineuses par analogie, une source de 1 candela produit la lumière d'une bougie. Cette valeur a bien sûr été normalisée pour pouvoir servir de référence. Elle est basée sur la puissance en watt émise sur une longueur d'onde précise au centre du spectre visible.
La lumière est émise dans plusieurs directions (voir toutes), donc il est nécessaire de tenir compte de cet aspect spatial pour quantifier l'émission lumineuse. Pour cette raison, le lumen a été créé. Un lumen représente la quantité de lumière qu'une bougie émettrait si tout ce qu'elle produit était concentré dans un cône d'un angle de base égal à environ 57,3° (un angle de 1 radian en fait).
Cet notion de quantification dans un cône n'est pas très pratique, on a donc défini la notion d'éclairement, mesuré en lux. L'éclairement est en quelque sorte la quantité d'eau que recevrait une feuille situé à un endroit précis par rapport à l'arrosage. Cet éclairement est reporté à la surface de la feuille, donc pour la lumière cela donne des lumens par mètre carré, qui représentent justement des lux.
Le lux est relatif à la lumière reçu, mais si on se place du point de vu de la source, une autre grandeur a été crée : la luminance (Brightness). Cette grandeur est un peu plus difficile à appréhender, donc nous allons utiliser pour cela un schéma:

L'aire verte n'est pas vue depuis le même endroit par les deux observateurs.
Celui placé au dessus voit cette zone sous sa forme réelle (sans l'effet de la perspective), et son aire apparente correspond à son aire réelle.
Celui placé de coté la voit avec une perspective qui lui donne un aspect plus ramassé et une aire apparente plus petite.
Alors que l'éclairement considère la quantité de lumière reçue par unité de surface au sens des aires jaune et bleue, la luminance détermine la quantité de lumière émise par unité de surface au sens de l'aire verte. De ce fait, en fonction de la forme de la source émettrice, l'éclairement reçu sera différent même si la distance entre la source et l'observateur reste identique. En effet, un carré plat se voir de plus en plus fin au fur et à mesure que notre point de vu se rapproche de sa tranche, alors qu'une boule aura toujours le même aspect (et donc la même surface apparente).
Si la distance entre le source et l'observateur varie, l'éclairement diminuera proportionnellement au carré de du rapport de distance. En effet, que l'on considère la lumière émise dans un cône ou une sphère (uni ou multi-directionnellement), la surface éclairée (base du cône ou aire de la sphère) sera toujours proportionnelle au carré de ses dimensions (hauteur ou diamètre). Pour comprendre cela il suffit de penser à un cube : il est constitué de 6 faces avec chacune une aire égale au produit de son coté par lui même, à son carré donc. Si on change la dimension de ce coté (en le multipliant par 2 par exemple), l'aire d'une face sera multipliée par le carré de ce facteur (2 fois 2). C'est la même chose pour le cône (πR²), la sphère (4πR²) et tout autre volume. Une conséquence de ce phénomène est que l'éclairement reçu à 1m d'une source de 1 candela (une bougie) est de 1 lux.
En photographie, il est capital de ne pas confondre l'éclairement et la luminance. Le premier est un flux reçu (quantité d'eau reçue depuis un point d'observation donné), et la seconde une quantité émise (débit de la source). L'analogie hydraulique n'aide plus vraiment la compréhension pour ces deux grandeurs car leur expression est surtout liée à la géométrie spatiale (les deux sont en fonction de m² mais sans que cela fasse référence à la même surface).
Le meilleur moyen de bien voir cette différence (et aussi de comprendre ce qui va suivre au sujet des photomètres) c'est d'essayer de comprendre la réponse à la question suivante : Quelle est la luminance d'un feuille de papier reçevant perpendiculairement à sa surface un éclairement de 100000 lux? (Cette feuille étant considérée comme réfléchissant toute la lumière reçue et ce de façon homogène dans toutes les directions)
Tous les détails de cette réponse sont sur dans cet article de Wikibook sur les sources orthotropes : http://fr.wikibooks.org/wiki/Photographie/Photom%C3%A9trie/Sources_orthotropes
La réponse à ce problème revient à calculer à quelle luminance correspond une source qui répartirait 100000 lux sur une demi-sphère selon le principe des aires apparentes décrit par la figure précédente.
La conclusion est que la luminance de la source est Pi (π) fois moins que l'éclairement reçu. Le facteur vient du fait que la feuille et plane, et que son aire apparente dépend du point de vu. Si cet objet réfléchissant avait la forme d'une sphère et réfléchissait de façon homogène dans toutes les directions un rayonnement incident de 100000 lux, sa luminance serait de 100000 candelas/m².
Pour résumer, nous avons vu les grandeurs suivantes: (Source: Lumière sur la lumière!)
Intensité d'une source lumineuse : Candela (une bougie ou 1/683 Watt par stéradian d'une radiation à 555nm)
Flux lumineux M : Lumen (1 lumen = 1 candela / stéradian)
Éclairement E : Lux (1 lux = 1 lumen / m²)
Luminance L : Candela / m²
Si la source a la même surface apparente et renvoie la même quantité de lumière dans toutes les directions, on a alors : L = E
Si la source renvoie la même quantité de lumière dans toutes les direction mais que c'est une surface plane : L = E / π
Et voici quelques repères en matière de valeurs d'éclairement:
L'indice de lumination (noté IL en français et EV en anglais) sert à caractériser la quantité de lumière issue d'une scène. Il peut se déterminer de deux manières : soit en mesurant la quantité de lumière incidente (qui éclaire le sujet), soit en mesurant la quantité de lumière réfléchie (qui repart en direction de l'appareil photo).
Dans les deux cas la formule est la même, excepté une constante, et elle permet de placer l'indice de lumination sur une échelle logarithmique.
Cette échelle, dont on a déjà parlé, revenait en quelque sorte à transformer un nombre en un autre représentant son nombre de zéros. Mille correspondait à 3, cent à 2 et ainsi de suite. Ceci était l'échelle logarithmique de base 10. Dix car ajouter 1 correspondait à multiplier par 10.
L'indice de lumination est représenté sur une échelle logarithmique de base 2. Donc ajouter 1 correspond à multiplier par 2.
Lorsqu'on dit qu'une image est exposée à +1IL par rapport à une autre, cela signifie qu'elle a reçu deux fois plus de lumière (ou que la surface fixatrice était deux fois plus sensible). Et lorsqu'on dit qu'une image est exposée à -1IL, c'est qu'elle a reçu deux fois moins de lumière.
Il existe également des demi et tiers d'IL, ils correspondent respectivement au facteurs racine carré de 2 environ égal à 1,44 et racine cubique de 2 environ égal à 1,26.
Pour obtenir cette échelle à partir de la luminance perçue (mesurée au niveau de l'appareil photo donc), on applique la formule suivante : IL = log2(L/0,3K)
Le terme L représente la luminance en candela/m², et le terme K est une constante qui dépend de la référence que l'on adopte (hé oui, dire qu'une photo est exposée à +0 IL est très subjectif!). Une valeur adoptée par certains photomètres est 11,4.
Pour obtenir l'indice de lumination à partir de l'éclairement (relatif à la lumière incidente au sujet et donc mesuré au niveau de celui-ci), on applique la formule suivante : IL = log2(E/0,3C)
Le terme E représente l'éclairement en lux et le terme C la constante de calibration du photomètre. Tout comme K, cette constante est subjective et dépend beaucoup de la nature du sujet car on a mesuré ici la lumière qui éclaire notre sujet, et pas celle qui atteint l'appareil photo. Une valeur de C adoptée par certains photomètre est 224.
Les deux formules de calcul de l'indice de lumination données ci-dessus sont presque identiques. On peut alors se demande à quoi corresponde le rapport C/K. (Source: Light meter, From Wikipedia)
Si on se souvient du calcul de la luminance de la feuille de papier exposée au soleil, on comprend que ce rapport doit avoir un lien avec le nombre Pi. Cependant 224/11,4 est égal à 6,25 fois le nombre Pi. Pourquoi?
C'est ici qu'intervient l'objectivité du réglage du photomètre. Ce facteur signifie que l'on considère que notre sujet renvoi 6,25 fois moins de lumière qu'il n'en a reçu, soit 16%. Cette valeur a été retenue car elle est proche de la moyenne des sujets que les photographes prennent en photo, mais elle sera trop forte dans le cas du portrait d'une personne noir et trop faibles si c'est une mariée en robe blanche.
Sources: Indice de lumination, from Wikipedia, Candela, from Wikipedia, Cours de Sandra Fiori, université de Montpellier
Faire de la photographie c'est écrire avec de la lumière, il semble donc naturel de pouvoir quantifier cette lumière. Pour cela, il est d'abord nécessaire de comprendre les différents concepts mis en jeux. Pour cela nous allons utiliser l'analogie hydraulique (encore elle).
Une source lumineuse émet de la lumière un peu comme un système d'arrosage émet de l'eau. On peut donc caractériser cette source par la quantité d'eau qu'elle émet, son intensité. Pour l'arrosage ça sera des litres par seconde, et pour la lumière des candela. Mais pourquoi n'utilise-t-on pas des truc par seconde dans le cas de la lumière? Parce que la lumière se comporte un peu comme une onde (comme des vagues ou un son) et un peu comme des particules (comme un jet d'eau). Donc il est impossible de la quantifier de la même façon que de l'eau. Il a donc été décidé de caractériser les sources lumineuses par analogie, une source de 1 candela produit la lumière d'une bougie. Cette valeur a bien sûr été normalisée pour pouvoir servir de référence. Elle est basée sur la puissance en watt émise sur une longueur d'onde précise au centre du spectre visible.
La lumière est émise dans plusieurs directions (voir toutes), donc il est nécessaire de tenir compte de cet aspect spatial pour quantifier l'émission lumineuse. Pour cette raison, le lumen a été créé. Un lumen représente la quantité de lumière qu'une bougie émettrait si tout ce qu'elle produit était concentré dans un cône d'un angle de base égal à environ 57,3° (un angle de 1 radian en fait).
Cet notion de quantification dans un cône n'est pas très pratique, on a donc défini la notion d'éclairement, mesuré en lux. L'éclairement est en quelque sorte la quantité d'eau que recevrait une feuille situé à un endroit précis par rapport à l'arrosage. Cet éclairement est reporté à la surface de la feuille, donc pour la lumière cela donne des lumens par mètre carré, qui représentent justement des lux.
Le lux est relatif à la lumière reçu, mais si on se place du point de vu de la source, une autre grandeur a été crée : la luminance (Brightness). Cette grandeur est un peu plus difficile à appréhender, donc nous allons utiliser pour cela un schéma:

L'aire verte n'est pas vue depuis le même endroit par les deux observateurs.
Celui placé au dessus voit cette zone sous sa forme réelle (sans l'effet de la perspective), et son aire apparente correspond à son aire réelle.
Celui placé de coté la voit avec une perspective qui lui donne un aspect plus ramassé et une aire apparente plus petite.
Alors que l'éclairement considère la quantité de lumière reçue par unité de surface au sens des aires jaune et bleue, la luminance détermine la quantité de lumière émise par unité de surface au sens de l'aire verte. De ce fait, en fonction de la forme de la source émettrice, l'éclairement reçu sera différent même si la distance entre la source et l'observateur reste identique. En effet, un carré plat se voir de plus en plus fin au fur et à mesure que notre point de vu se rapproche de sa tranche, alors qu'une boule aura toujours le même aspect (et donc la même surface apparente).
Si la distance entre le source et l'observateur varie, l'éclairement diminuera proportionnellement au carré de du rapport de distance. En effet, que l'on considère la lumière émise dans un cône ou une sphère (uni ou multi-directionnellement), la surface éclairée (base du cône ou aire de la sphère) sera toujours proportionnelle au carré de ses dimensions (hauteur ou diamètre). Pour comprendre cela il suffit de penser à un cube : il est constitué de 6 faces avec chacune une aire égale au produit de son coté par lui même, à son carré donc. Si on change la dimension de ce coté (en le multipliant par 2 par exemple), l'aire d'une face sera multipliée par le carré de ce facteur (2 fois 2). C'est la même chose pour le cône (πR²), la sphère (4πR²) et tout autre volume. Une conséquence de ce phénomène est que l'éclairement reçu à 1m d'une source de 1 candela (une bougie) est de 1 lux.
En photographie, il est capital de ne pas confondre l'éclairement et la luminance. Le premier est un flux reçu (quantité d'eau reçue depuis un point d'observation donné), et la seconde une quantité émise (débit de la source). L'analogie hydraulique n'aide plus vraiment la compréhension pour ces deux grandeurs car leur expression est surtout liée à la géométrie spatiale (les deux sont en fonction de m² mais sans que cela fasse référence à la même surface).
Le meilleur moyen de bien voir cette différence (et aussi de comprendre ce qui va suivre au sujet des photomètres) c'est d'essayer de comprendre la réponse à la question suivante : Quelle est la luminance d'un feuille de papier reçevant perpendiculairement à sa surface un éclairement de 100000 lux? (Cette feuille étant considérée comme réfléchissant toute la lumière reçue et ce de façon homogène dans toutes les directions)
Tous les détails de cette réponse sont sur dans cet article de Wikibook sur les sources orthotropes : http://fr.wikibooks.org/wiki/Photographie/Photom%C3%A9trie/Sources_orthotropes
La réponse à ce problème revient à calculer à quelle luminance correspond une source qui répartirait 100000 lux sur une demi-sphère selon le principe des aires apparentes décrit par la figure précédente.
La conclusion est que la luminance de la source est Pi (π) fois moins que l'éclairement reçu. Le facteur vient du fait que la feuille et plane, et que son aire apparente dépend du point de vu. Si cet objet réfléchissant avait la forme d'une sphère et réfléchissait de façon homogène dans toutes les directions un rayonnement incident de 100000 lux, sa luminance serait de 100000 candelas/m².
Pour résumer, nous avons vu les grandeurs suivantes: (Source: Lumière sur la lumière!)
Intensité d'une source lumineuse : Candela (une bougie ou 1/683 Watt par stéradian d'une radiation à 555nm)
Flux lumineux M : Lumen (1 lumen = 1 candela / stéradian)
Éclairement E : Lux (1 lux = 1 lumen / m²)
Luminance L : Candela / m²
Si la source a la même surface apparente et renvoie la même quantité de lumière dans toutes les directions, on a alors : L = E
Si la source renvoie la même quantité de lumière dans toutes les direction mais que c'est une surface plane : L = E / π
Et voici quelques repères en matière de valeurs d'éclairement:
- à 1m d'une bougie comme seule source lumineuse : 1 lux
- local de vie : 100 à 200 lux
- local de travail : 200 à 3 000 lux
- stade de nuit : 1 500 lux
- journée ensoleillée : 50 000 à 100 000 lux
L'indice de lumination (noté IL en français et EV en anglais) sert à caractériser la quantité de lumière issue d'une scène. Il peut se déterminer de deux manières : soit en mesurant la quantité de lumière incidente (qui éclaire le sujet), soit en mesurant la quantité de lumière réfléchie (qui repart en direction de l'appareil photo).
Dans les deux cas la formule est la même, excepté une constante, et elle permet de placer l'indice de lumination sur une échelle logarithmique.
Cette échelle, dont on a déjà parlé, revenait en quelque sorte à transformer un nombre en un autre représentant son nombre de zéros. Mille correspondait à 3, cent à 2 et ainsi de suite. Ceci était l'échelle logarithmique de base 10. Dix car ajouter 1 correspondait à multiplier par 10.
L'indice de lumination est représenté sur une échelle logarithmique de base 2. Donc ajouter 1 correspond à multiplier par 2.
Lorsqu'on dit qu'une image est exposée à +1IL par rapport à une autre, cela signifie qu'elle a reçu deux fois plus de lumière (ou que la surface fixatrice était deux fois plus sensible). Et lorsqu'on dit qu'une image est exposée à -1IL, c'est qu'elle a reçu deux fois moins de lumière.
Il existe également des demi et tiers d'IL, ils correspondent respectivement au facteurs racine carré de 2 environ égal à 1,44 et racine cubique de 2 environ égal à 1,26.
Pour obtenir cette échelle à partir de la luminance perçue (mesurée au niveau de l'appareil photo donc), on applique la formule suivante : IL = log2(L/0,3K)
Le terme L représente la luminance en candela/m², et le terme K est une constante qui dépend de la référence que l'on adopte (hé oui, dire qu'une photo est exposée à +0 IL est très subjectif!). Une valeur adoptée par certains photomètres est 11,4.
Pour obtenir l'indice de lumination à partir de l'éclairement (relatif à la lumière incidente au sujet et donc mesuré au niveau de celui-ci), on applique la formule suivante : IL = log2(E/0,3C)
Le terme E représente l'éclairement en lux et le terme C la constante de calibration du photomètre. Tout comme K, cette constante est subjective et dépend beaucoup de la nature du sujet car on a mesuré ici la lumière qui éclaire notre sujet, et pas celle qui atteint l'appareil photo. Une valeur de C adoptée par certains photomètre est 224.
Les deux formules de calcul de l'indice de lumination données ci-dessus sont presque identiques. On peut alors se demande à quoi corresponde le rapport C/K. (Source: Light meter, From Wikipedia)
Si on se souvient du calcul de la luminance de la feuille de papier exposée au soleil, on comprend que ce rapport doit avoir un lien avec le nombre Pi. Cependant 224/11,4 est égal à 6,25 fois le nombre Pi. Pourquoi?
C'est ici qu'intervient l'objectivité du réglage du photomètre. Ce facteur signifie que l'on considère que notre sujet renvoi 6,25 fois moins de lumière qu'il n'en a reçu, soit 16%. Cette valeur a été retenue car elle est proche de la moyenne des sujets que les photographes prennent en photo, mais elle sera trop forte dans le cas du portrait d'une personne noir et trop faibles si c'est une mariée en robe blanche.
Méthode de calcul du temps d'exposition (Lien)
Source: The Pumpkin, a library of selected writings of Douglas A. Kerr
La méthode APEX tient son nom de "Additive System for Photographic Exposure" car elle repose sur une formule toute simple mais incroyablement utile:
Av + Tv = Bv + Sv
Mais que veulent dire ces quatre termes?
Vous vous en doutez peut-être, mais ce sont toutes des grandeur logarithmiques (par rapport aux grandeurs physiques).
Av est l'"Aperture value", ou valeur d'ouverture. On a vu que le nombre d'ouverture était une surface reportée à une unité de longueur focale : f/D, Av est cette même valeur reportée sur une échelle logarithmique, soit : Av = 2 log2(f/D)
f/D c'est le nombre d'ouverture, ok. Log2 c'est pour avoir une échelle logarithmique en base 2, d'accord. Mais pourquoi on multiplie par 2? Parce que f/D est homogène à une longueur, et que lorsqu'on double une longueur, la surface (et donc le flux lumineux) est multiplié par 4 (le carré de 2).
Prenez un carré de 1m de coté. Son aire est de 1m².
Agrandissez votre carré pour qu'il fasse 2m de coté. Son aire est maintenant de 2x2=4m².
Comme la quantité de lumière qui passe au travers du trou du diaphragme est proportionnel à l'air de celui-ci (c'est du pur bon sens), alors doubler son diamètre (donc le nombre d'ouverture) reviens à multiplier par 4 la quantité de lumière, d'où le facteur 2 devant le logarithme.
Dernier détail avant de passer au terme suivant : Où est la touche log2 sur la calculatrice? Nulle part. Le logarithme de base N se calcul de la façon suivante à partir du logarithme de base e (noté ln) : LogN x = ln x / ln N.
Par exemple : pour f/2.8, on a Av = 2 Log2(f/D) = 2 Log2(2,8) = 2 * 1,485 = 2,97
Tv est la "Time value", ou temps d'exposition. Lui aussi sur une échelle logarithmique de base 2.
Sa valeur est l'opposé sur logarithme de la durée d'exposition.
Par exemple : pour 1/8s, on a Tv = -Log2(1/8) = -Log2(0,125) = -(-3) = 3
Sv est la "Speed value", ou sensibilité de la surface fixatrice. Également sur une échelle logarithmique de base 2, Sv est égal à Log2(S/3,125) où S est la sensibilité en nombre ISO.
Par exemple : pour 100ISO, on a Sv = Log2(100/3,125) = Log2(32) = 5
Bv est la "Brightness value", ou valeur de luminosité. Elle correspond à l'indice de lumination dont on a parlé dans la partie précédente. Pour rappel, on peut la calculer à partir de la luminance:
Bv=log2(L/0,3K) avec L en candela/m² et K=11,4 (pour certains photomètres)
Ou de l'éclairement incident du sujet. Dans ce cas le terme de la formule APEX n'est plus noté Bv mais Iv pour "Incident value":
Iv=log2(E/0,3C) avec E en lux et C=224 (pour certains photomètres)
De nos jours, la formule APEX n'est plus utile du fait de la performance des mesures automatiques d'exposition faite par les appareils photos, ainsi que de la possibilité qu'offre le numérique de voir et de refaire le cliché immédiatement.
Cependant, une information importante est à retenir de cette formule : Av possède, contrairement à Tv et Sv un facteur 2 devant le Log. Ceci signifie que si on double le temps de pause ou la sensibilité, on gagnera +1IL, mais si on double l'ouverture, on en gagnera 2.
C'est pour cette raison que l'ouverture maximum qu'un objectif peut atteindre est si important pour pouvoir photographier en faible lumière. Ces 2IL sont tout spécialement important quand on doit faire le choix entre un objectif à focale fixe qui ouvre jusqu'à f1.4 et un zoom qui ne peut atteindre que f2.8, d'autant plus que le premier et généralement moins cher que le second.
Pour terminer, je vais lever le voile sur quelque chose qui est peut-être un mystère pour certains : 1, 1.1, 1.2, 1.4, 1.6, 1.8, 2, 2.2, 2.5, 2.8, 3.2, 3.5, 4, 4.5, 5, 5.6, 6.3, 7.1, 8... ça vous dit quelque chose? Certes, mais pourquoi ces nombres?
La réponse se trouve dans les puissances de 2. On vient de voir que doubler la quantité de lumière c'est gagner 1IL, et que doubler l'ouverture permet de gagner 2IL. Les nombres d'ouverture ont donc été choisis en tenant compte de ce phénomène. Arbitrairement, et sûrement parce que l'on s'est rendu compte que cela suffisait, les IL on été divisés en trois, donc les nombres d'ouverture en 6. Ainsi, on aura 6 crans de réglage pour passer d'un nombre d'ouverture à son double. Mais comment faire pour que cette échelle soit homogène sur ces six crans? On multiplie par 2/6 à chaque fois? Non, parce que (2/6)^6 ça ne fait pas 2, or on a vu que tout était question de rapport de multiplication en ce qui concerne la lumière. En revanche (2^(1/6))^6 ça fait bien 2. L'échelle des nombres d'ouverture est donc une progression de facteur 2^(1/6)=1.122462...
Pour construire cette échelle, on part donc de 1 et on multiplie à chaque fois par ce nombre. On trouve alors, à un arrondi près, la suite des nombres d'ouverture.
Fidèle à la méthode APEX, les temps de pause et les ISO suivent (presque) cette même progression. Je dis presque parce que dans le cas des ISO, l'argentique héritant l'ISO de la pellicule, pas besoin d'avoir des tiers d'IL, donc les valeurs ISO vont simplement de double en double en partant de 100 : 200, 400, 800, 1600, 3200.
Pour les temps de pause en revanche, on a bien les tiers d'IL à partir de 1 seconde, soit 1 seconde, 1/2^(1/3)=0.8, 1/(2^(1/3)^2)=0.6 seconde, 1/(2^(1/3)^3)=0.5 seconde et ainsi de suite.
En fait, les valeurs de diaphragme et de temps de pause se compensent, si on augmente d'un cran la valeur d'ouverture, on peut le compenser en réduisant d'un cran le temps de pause. Pour cette raison, les photographes parlent souvent de "diaph" en parlant d'exposition. Par exemple: "entre le visage et le décor j'ai deux diaph". Ceci veut dire que la différence de quantité de lumière entre celle provenant du visage et celle du décor est de deux fois un tiers d'IL, soit un rapport de (2^(1/3))^2=1.5874. Avec l'expérience, on peut alors mettre en place les éclairages de la scène qu'on photographie et avoir une idée du résultat uniquement en mesurant le nombre de "diaph" de différence que l'on a entre toutes les parties de la future image, un peu comme un musicien a une idée d'une mélodie en lisant des notes sur une portée.
Source: The Pumpkin, a library of selected writings of Douglas A. Kerr
La méthode APEX tient son nom de "Additive System for Photographic Exposure" car elle repose sur une formule toute simple mais incroyablement utile:
Av + Tv = Bv + Sv
Mais que veulent dire ces quatre termes?
Vous vous en doutez peut-être, mais ce sont toutes des grandeur logarithmiques (par rapport aux grandeurs physiques).
Av est l'"Aperture value", ou valeur d'ouverture. On a vu que le nombre d'ouverture était une surface reportée à une unité de longueur focale : f/D, Av est cette même valeur reportée sur une échelle logarithmique, soit : Av = 2 log2(f/D)
f/D c'est le nombre d'ouverture, ok. Log2 c'est pour avoir une échelle logarithmique en base 2, d'accord. Mais pourquoi on multiplie par 2? Parce que f/D est homogène à une longueur, et que lorsqu'on double une longueur, la surface (et donc le flux lumineux) est multiplié par 4 (le carré de 2).
Prenez un carré de 1m de coté. Son aire est de 1m².
Agrandissez votre carré pour qu'il fasse 2m de coté. Son aire est maintenant de 2x2=4m².
Comme la quantité de lumière qui passe au travers du trou du diaphragme est proportionnel à l'air de celui-ci (c'est du pur bon sens), alors doubler son diamètre (donc le nombre d'ouverture) reviens à multiplier par 4 la quantité de lumière, d'où le facteur 2 devant le logarithme.
Dernier détail avant de passer au terme suivant : Où est la touche log2 sur la calculatrice? Nulle part. Le logarithme de base N se calcul de la façon suivante à partir du logarithme de base e (noté ln) : LogN x = ln x / ln N.
Par exemple : pour f/2.8, on a Av = 2 Log2(f/D) = 2 Log2(2,8) = 2 * 1,485 = 2,97
Tv est la "Time value", ou temps d'exposition. Lui aussi sur une échelle logarithmique de base 2.
Sa valeur est l'opposé sur logarithme de la durée d'exposition.
Par exemple : pour 1/8s, on a Tv = -Log2(1/8) = -Log2(0,125) = -(-3) = 3
Sv est la "Speed value", ou sensibilité de la surface fixatrice. Également sur une échelle logarithmique de base 2, Sv est égal à Log2(S/3,125) où S est la sensibilité en nombre ISO.
Par exemple : pour 100ISO, on a Sv = Log2(100/3,125) = Log2(32) = 5
Bv est la "Brightness value", ou valeur de luminosité. Elle correspond à l'indice de lumination dont on a parlé dans la partie précédente. Pour rappel, on peut la calculer à partir de la luminance:
Bv=log2(L/0,3K) avec L en candela/m² et K=11,4 (pour certains photomètres)
Ou de l'éclairement incident du sujet. Dans ce cas le terme de la formule APEX n'est plus noté Bv mais Iv pour "Incident value":
Iv=log2(E/0,3C) avec E en lux et C=224 (pour certains photomètres)
De nos jours, la formule APEX n'est plus utile du fait de la performance des mesures automatiques d'exposition faite par les appareils photos, ainsi que de la possibilité qu'offre le numérique de voir et de refaire le cliché immédiatement.
Cependant, une information importante est à retenir de cette formule : Av possède, contrairement à Tv et Sv un facteur 2 devant le Log. Ceci signifie que si on double le temps de pause ou la sensibilité, on gagnera +1IL, mais si on double l'ouverture, on en gagnera 2.
C'est pour cette raison que l'ouverture maximum qu'un objectif peut atteindre est si important pour pouvoir photographier en faible lumière. Ces 2IL sont tout spécialement important quand on doit faire le choix entre un objectif à focale fixe qui ouvre jusqu'à f1.4 et un zoom qui ne peut atteindre que f2.8, d'autant plus que le premier et généralement moins cher que le second.
Pour terminer, je vais lever le voile sur quelque chose qui est peut-être un mystère pour certains : 1, 1.1, 1.2, 1.4, 1.6, 1.8, 2, 2.2, 2.5, 2.8, 3.2, 3.5, 4, 4.5, 5, 5.6, 6.3, 7.1, 8... ça vous dit quelque chose? Certes, mais pourquoi ces nombres?
La réponse se trouve dans les puissances de 2. On vient de voir que doubler la quantité de lumière c'est gagner 1IL, et que doubler l'ouverture permet de gagner 2IL. Les nombres d'ouverture ont donc été choisis en tenant compte de ce phénomène. Arbitrairement, et sûrement parce que l'on s'est rendu compte que cela suffisait, les IL on été divisés en trois, donc les nombres d'ouverture en 6. Ainsi, on aura 6 crans de réglage pour passer d'un nombre d'ouverture à son double. Mais comment faire pour que cette échelle soit homogène sur ces six crans? On multiplie par 2/6 à chaque fois? Non, parce que (2/6)^6 ça ne fait pas 2, or on a vu que tout était question de rapport de multiplication en ce qui concerne la lumière. En revanche (2^(1/6))^6 ça fait bien 2. L'échelle des nombres d'ouverture est donc une progression de facteur 2^(1/6)=1.122462...
Pour construire cette échelle, on part donc de 1 et on multiplie à chaque fois par ce nombre. On trouve alors, à un arrondi près, la suite des nombres d'ouverture.
Fidèle à la méthode APEX, les temps de pause et les ISO suivent (presque) cette même progression. Je dis presque parce que dans le cas des ISO, l'argentique héritant l'ISO de la pellicule, pas besoin d'avoir des tiers d'IL, donc les valeurs ISO vont simplement de double en double en partant de 100 : 200, 400, 800, 1600, 3200.
Pour les temps de pause en revanche, on a bien les tiers d'IL à partir de 1 seconde, soit 1 seconde, 1/2^(1/3)=0.8, 1/(2^(1/3)^2)=0.6 seconde, 1/(2^(1/3)^3)=0.5 seconde et ainsi de suite.
En fait, les valeurs de diaphragme et de temps de pause se compensent, si on augmente d'un cran la valeur d'ouverture, on peut le compenser en réduisant d'un cran le temps de pause. Pour cette raison, les photographes parlent souvent de "diaph" en parlant d'exposition. Par exemple: "entre le visage et le décor j'ai deux diaph". Ceci veut dire que la différence de quantité de lumière entre celle provenant du visage et celle du décor est de deux fois un tiers d'IL, soit un rapport de (2^(1/3))^2=1.5874. Avec l'expérience, on peut alors mettre en place les éclairages de la scène qu'on photographie et avoir une idée du résultat uniquement en mesurant le nombre de "diaph" de différence que l'on a entre toutes les parties de la future image, un peu comme un musicien a une idée d'une mélodie en lisant des notes sur une portée.





